
 已知:如图,直线与两坐标轴相交于A、B两点,
已知:如图,直线与两坐标轴相交于A、B两点,科目:初中数学 来源:2013年初中毕业升学考试(湖北荆州卷)数学(解析版) 题型:解答题
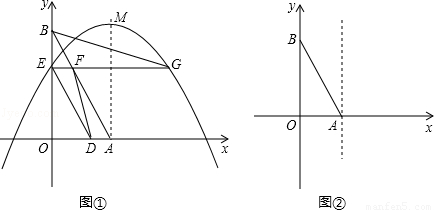
如图,已知:如图①,直线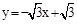 与x轴、y轴分别交于A、B两点,两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止);对称轴过点A且顶点为M的抛物线
与x轴、y轴分别交于A、B两点,两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止);对称轴过点A且顶点为M的抛物线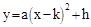 (a<0)始终经过点E,过E作EG∥OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位长度/秒和
(a<0)始终经过点E,过E作EG∥OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位长度/秒和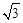 个单位长度/秒,运动时间为t秒.
个单位长度/秒,运动时间为t秒.
(1)用含t代数式分别表示BF、EF、AF的长;
(2)当t为何值时,四边形ADEF是菱形?判断此时△AFG与△AGB是否相似,并说明理由;
(3)当△ADF是直角三角形,且抛物线的顶点M恰好在BG上时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:2002年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点.
与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点.
查看答案和解析>>
科目:初中数学 来源:2002年河南省中考数学试卷(解析版) 题型:解答题
 与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点.
与x轴、y轴分别交于A、B两点,⊙M经过原点O及A、B两点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com