
��ͼ����֪����ͼ�٣�ֱ�� ��x�ᡢy��ֱ���A��B���㣬������D��E�ֱ��A��B����ͬʱ������O���˶����˶���O��ֹͣ�����Գ������A�Ҷ���ΪM��������
��x�ᡢy��ֱ���A��B���㣬������D��E�ֱ��A��B����ͬʱ������O���˶����˶���O��ֹͣ�����Գ������A�Ҷ���ΪM��������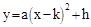 ��a��0��ʼ�վ�����E����E��EG��OA���������ڵ�G����AB�ڵ�F������DE��DF��AG��BG����D��E���˶��ٶȷֱ���1����λ����/���
��a��0��ʼ�վ�����E����E��EG��OA���������ڵ�G����AB�ڵ�F������DE��DF��AG��BG����D��E���˶��ٶȷֱ���1����λ����/���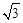 ����λ����/�룬�˶�ʱ��Ϊt�룮
����λ����/�룬�˶�ʱ��Ϊt�룮
��1���ú�t����ʽ�ֱ��ʾBF��EF��AF�ij���
��2����tΪ��ֵʱ���ı���ADEF�����Σ��жϴ�ʱ��AFG���AGB�Ƿ����ƣ���˵�����ɣ�
��3������ADF��ֱ�������Σ��������ߵĶ���Mǡ����BG��ʱ���������ߵĽ���ʽ��
�⣺��1����ֱ�߽���ʽ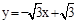 �У���x=0����y=
����x=0����y=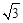 ����y=0����x=1��
����y=0����x=1��
��A��1��0����B��0��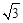 ����OA=1��OB=
����OA=1��OB=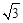 ��
��
��tan��OAB=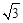 �����OAB=60�㡣��AB=2OA=2��
�����OAB=60�㡣��AB=2OA=2��
��EG��OA�����EFB=��OAB=60�㡣
��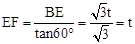 ��BF=2EF=2t��
��BF=2EF=2t��
��AF=AB��BF=2��2t��
��2���١�EF��AD����EF=AD=t�����ı���ADEFΪƽ���ı��Ρ�
��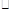 ADEF��������DE=AD=t��
ADEF��������DE=AD=t��
��DE=2OD������t=2��1��t�������t=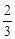 ��
��
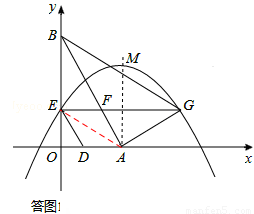
��t=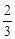 ʱ���ı���ADEF�����Ρ�
ʱ���ı���ADEF�����Ρ�
�ڴ�ʱ��AFG���AGB���ơ��������£�
���ͼ1��ʾ������AE��
���ı���ADEF�����Σ�
���DEF=��DAF=60�㡣���AEF=30�㡣
�������ߵĶԳ��Կ�֪��AG=AE��
���AGF=��AEF=30�㡣
��Rt��BEG��BE=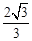 ��EG=2��
��EG=2��
�� �����EBG=60�㡣
�����EBG=60�㡣
���ABG=��EBG����EBF=30�㡣
�ڡ�AFG���AGB�У��ߡ�BAG=��GAF����ABG=��AGF=30�㣬
���AFG�ס�AGB��
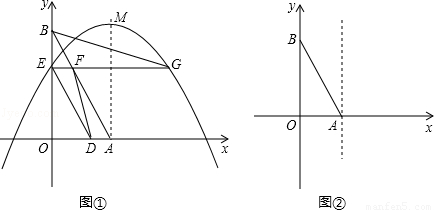
��3������ADF��ֱ��������ʱ��
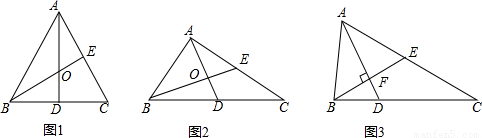
������ADF=90�㣬���ͼ2��ʾ��
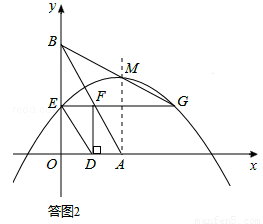
��ʱAF=2DA����2��2t=2t�����t=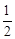 ��
��
��BE=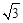 t=
t=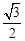 ��OE=OB��BE=
��OE=OB��BE=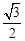 ��
��
��E��0��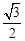 ����G��2��
����G��2��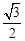 ����
����
��ֱ��BG�Ľ���ʽΪy=kx+b��
��B��0��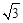 ����G��2��
����G��2��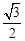 ������ã�
������ã�
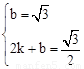 �����
�����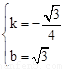 ��
��
��ֱ��BG�Ľ���ʽΪ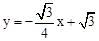 ��
��
��x=1����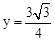 ����M��1��
����M��1��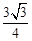 ����
����
�������߽���ʽΪ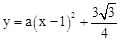 ��
��
�ߵ�E��0��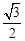 �����������ϣ�
�����������ϣ�
��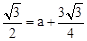 �����
�����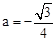 ��
��
�������߽���ʽΪ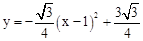 ����
����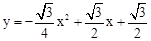 ��
��
������AFD=90�㣬���ͼ3��ʾ��
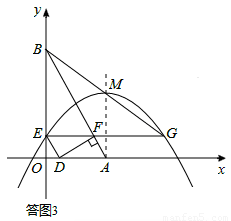
��ʱAD=2AF������t=2��2��2t������ã�t=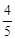 ��
��
��BE=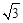 t=
t=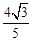 ��OE=OB��BE=
��OE=OB��BE=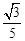 ��
��
��E��0��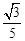 ����G��2��
����G��2��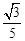 ����
����
��ֱ��BG�Ľ���ʽΪy=k1x+b1��
��B��0��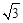 ����G��2��
����G��2��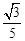 ������ã�
������ã�
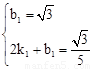 �����
�����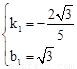 ��
��
��ֱ��BG�Ľ���ʽΪ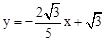 ��
��
��x=1����y=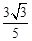 ����M��1��
����M��1��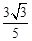 ����
����
�������߽���ʽΪ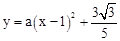 ��
��
�ߵ�E��0��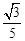 �����������ϣ�
�����������ϣ�
��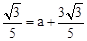 �����
�����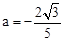 ��
��
�������߽���ʽΪ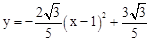 ����
����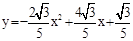 ��
��
�������������������������ߵĽ���ʽΪ��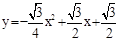 ��
��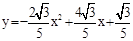
��������
�����������1���������һ�κ��� �������ύ��A��B�����꣬Ȼ���ֱ�����������BF��EF��AF�ij���
�������ύ��A��B�����꣬Ȼ���ֱ�����������BF��EF��AF�ij���
��2����EF��AD����EF=AD=t�����ı���ADEFΪƽ���ı��Σ���▱ADEF�����Σ���DE=AD=t����DE=2OE���з������t��ֵ��
���ͼ1��ʾ���Ƴ���BAG=��GAF����ABG=��AGF=30�㣬֤����AFG���AGB���ơ�
��3������ADF��ֱ��������ʱ�����������Σ���Ҫ�������ۣ�
������ADF=90�㣬���ͼ2��ʾ�����������ʱt��ֵ����������G�����꣬���ô���ϵ�������ֱ��BG�Ľ���ʽ���õ���M�����꣬������ö���ʽ�ʹ���ϵ������������ߵĽ���ʽ��
������AFD=90�㣬���ͼ3��ʾ������˼·�����ͬ��


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 21����֪����ͼ����������ABCD�У���E��BC�ߵ��е㣬����AE���ӳ���CD���ӳ������G��
21����֪����ͼ����������ABCD�У���E��BC�ߵ��е㣬����AE���ӳ���CD���ӳ������G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
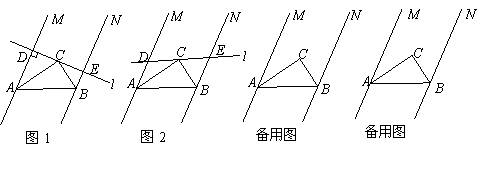
��֪����ͼ��ʾ��ֱ��![]() ��
��![]() ��ƽ���߽��ڵ�
��ƽ���߽��ڵ�![]() ������
������![]() ��һ��ֱ��
��һ��ֱ��![]() ������ֱ��
������ֱ��![]() �ֱ��ཻ�ڵ�
�ֱ��ཻ�ڵ�![]() ��
��
��1����ͼ1��ʾ����ֱ��![]() ��ֱ��
��ֱ��![]() ��ֱʱ�������߶�
��ֱʱ�������߶�![]() ֮���������ϵ����ֱ��д�����ۣ�����֤����
֮���������ϵ����ֱ��д�����ۣ�����֤����
��2����ͼ2��ʾ����ֱ��![]() ��ֱ��
��ֱ��![]() ����ֱ�ҽ���
����ֱ�ҽ���![]() ����
����![]() ��ͬ��ʱ����1���еĽ����Ƿ�����������������֤�����������������˵�����ɣ�
��ͬ��ʱ����1���еĽ����Ƿ�����������������֤�����������������˵�����ɣ�
��3����ֱ��![]() ��ֱ��
��ֱ��![]() ����ֱ�ҽ���
����ֱ�ҽ���![]() ��
��![]() �����ʱ����1���еĽ����Ƿ���Ȼ�����������������˵�����ɣ��������������ô�߶�
�����ʱ����1���еĽ����Ƿ���Ȼ�����������������˵�����ɣ��������������ô�߶�![]() ֮�仹����ij��������ϵ��������ڣ���ֱ��д������֮���������ϵ��
֮�仹����ij��������ϵ��������ڣ���ֱ��д������֮���������ϵ��
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�걱���з�ɽ���п���ѧ��ģ�Ծ��������棩 ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com