
【题目】已知x= ![]() ,y=
,y= ![]() ,求代数式(x+y)2﹣(x﹣y)2的值.
,求代数式(x+y)2﹣(x﹣y)2的值.
【答案】解:原式=(x+y+x﹣y)(x+y﹣x+y) =2x2y
=4xy.
当x= ![]() ,y=
,y= ![]() 时,原式=4×
时,原式=4× ![]() ×
× ![]() =
= ![]()
【解析】本题虽是一道计算题,但应该根据式子特点选择合适的方法,其实质考查的仍是运用公式法进行因式分解的能力,观察式子x、y都是分数,直接代数求值很麻烦,可采用先因式分解,再代数求值的方法.
【考点精析】本题主要考查了代数式求值和因式分解的应用的相关知识点,需要掌握求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入;因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】(本题满分10分)
一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金
x(元)与每月租出的车辆数(y)有如下关系:
x | 4500 | 4000 | 3800 | 3200 |
y | 70 | 80 | 84 | 96 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元. 每辆车的月租金定为多少元时,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过坐标原点,与
的图象经过坐标原点,与![]() 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).

(1)求二次函数的解析式
(2)在抛物线上是否存在一点P,使△AOP的面积为3,若存在请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在一次抽奖活动中,“中奖概率是![]() ”表示抽奖100次就一定会中奖
”表示抽奖100次就一定会中奖
B.随机抛一枚硬币,落地后正面一定朝上
C.同时掷两枚均匀的骰子,朝上一面的点数和为6
D.在一副没有大小王的扑克牌中任意抽一张,抽到的牌是6的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与双曲线
与双曲线![]() 全相交于点A、B,且抛物线经过坐标原点,点
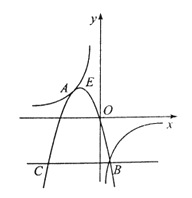
全相交于点A、B,且抛物线经过坐标原点,点![]() 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
(1)求双曲线和抛物线的解析式;
(2)计算![]() 与
与![]() 的面积;
的面积;
(3)在抛物线上是否存在点D,使![]() 的面积等于
的面积等于![]() 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
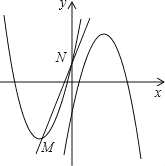
【题目】如图,在平面直角坐标系中,已知抛物线C1:y=![]() 的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
(1)结合图象,直接写出不等式![]() x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;
(2)若抛物线C2的顶点与点M关于原点对称,求p的值及抛物线C2的解析式;
(3)若直线l沿y轴向下平移q个单位长度后,与(2)中的抛物线C2存在公共点,
求3﹣4q的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com