练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列命题中，正确的有（ ）

    ①平分弦的直径垂直于弦；

    ②三角形的三个顶点确定一个圆；

    ③圆内接四边形的对角相等；

    ④圆的切线垂直于过切点的半径；

    ⑤过圆外一点所画的圆的两条切线长相等．

    A.1个B.2个C.3个D.4个

    【答案】D

    【解析】

    试题平分弦（非直径）的直径垂直于弦，所以①错误；

    三角形的三个顶点确定一个圆，所以②正确；

    圆内接四边形的对角互补，所以③正确；

    圆的切线垂直于过切点的半径，所以④正确；

    过圆外一点所画的圆的两条切线长相等，所以⑤正确．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】(2016山东潍坊第18题)在平面直角坐标系中，直线l：y=x﹣1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点Bn的坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球，乒乓球拍每副定价元，乒乓球每盒定价元，现两家商店搞促销活动，甲店：每买一副乒乓球拍赠送一盒乒乓球；乙店：按定价的九折优惠．某人需购球拍副，乒乓球若干盒（不少于盒）．

    （）设购买乒乓球盒数为（盒），在甲商店付款为（元），在乙商店付款为（元），分别写出， 与的关系式．

    （）就乒乓球盒数讨论去哪家商店买更优惠．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．

    下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．

    证明：在边AB上截取AE=MC，连ME．

    正方形ABCD中，∠B=∠BCD=90°，AB=BC．

    ∴∠NMC=180°—∠AMN—∠AMB

    =180°—∠B—∠AMB

    =∠MAB=∠MAE．

    （下面请你完成余下的证明过程）

    （2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

    （3）若将（1）中的“正方形ABCD”改为“正边形ABCD…X”，请你作出猜想：当∠AMN=°时，结论AM=MN仍然成立．（直接写出答案，不需要证明）

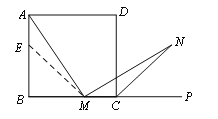
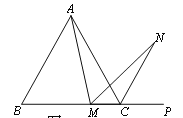
    图1 图2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下表记录了甲、乙、丙、丁四名八年级学生最近几次校数学竞赛成绩的平均数与方差：

    甲

    乙

    丙

    丁

    平均数（分）

    115

    110

    115

    110

    方差

    3.4

    3.4

    7.3

    8.5

    根据表中数据，要从中选择一名成绩好且发挥稳定的学生参加市数学竞赛，应该选择（ ）

    A.甲B.乙C.丙D.丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果5akb与-4a2b是同类项，那么5akb+（-4a2b）=_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】测量计算是日常生活中常见的问题，如图，建筑物BC的屋顶有一根旗杆AB，从地面上D点处观测旗杆顶点A的仰角为50°，观测旗杆底部B点的仰角为45°，（可用的参考数据：sin50°≈0.8，tan50°≈1.2）

    （1）若已知CD=20米，求建筑物BC的高度；（2）若已知旗杆的高度AB=5米，求建筑物BC的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：5x2x4﹣（﹣2x3）2+x8÷x2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(2016山东潍坊第23题)旅游公司在景区内配置了50辆观光车共游客租赁使用，假定每辆观光车一天内最多只能出租一次，且每辆车的日租金x（元）是5的倍数．发现每天的营运规律如下：当x不超过100元时，观光车能全部租出；当x超过100元时，每辆车的日租金每增加5元，租出去的观光车就会减少1辆．已知所有观光车每天的管理费是1100元．

    （1）优惠活动期间，为使观光车全部租出且每天的净收入为正，则每辆车的日租金至少应为多少元？（注：净收入=租车收入﹣管理费）

    （2）当每辆车的日租金为多少元时，每天的净收入最多？

    查看答案和解析>>

    同步练习册答案