
(8分)已知,如图1, 中,
中, ,
, 是平面内不与
是平面内不与 、
、 、
、 重合的任意一点,
重合的任意一点, ,
, .
.

(1)求证: ≌
≌ ;
;
(2)如图2,当点 是
是 的外接圆圆心时,请判断四边形
的外接圆圆心时,请判断四边形 的形状,并证明你的结论.
的形状,并证明你的结论.
(1)见解析;
(2)四边形BDCE是菱形,证明见解析.
【解析】
试题分析:(1)由∠ABC=∠DBE可知∠ABC+∠CBD=∠DBE+∠CBD,即∠ABD=∠CBE,根据SAS定理可知△ABD≌△CBE;
(2)由(1)可知,△ABD≌△CBE,故CE=AD,根据点D是△ABC外接圆圆心可知DA=DB=DC,再由BD=BE可判断出BD=BE=CE=CD,故可得出四边形BDCE是菱形.
(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBD=∠DBE+∠CBD,
∴∠ABD=∠CBE,
在△ABD与△CBE中,
∵
∴△ABD≌△CBE
(2)解:四边形BDCE是菱形.证明如下:
同(1)可证△ABD≌△CBE,
∴CE=AD,
∵点D是△ABC外接圆圆心,
∴DA=DB=DC,
又∵BD=BE,
∴BD=BE=CE=CD,
∴四边形BDCE是菱形.
考点:三角形的外接圆与外心;全等三角形的判定与性质;菱形的判定.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.

科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(1)(4分)计算: .
.
(2)(5分)已知关于x的一元二次方程 有两个相等的实数根,求
有两个相等的实数根,求 的值。
的值。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(本题8分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.

(1)断⊿BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:填空题
已知三角形两边的长分别是3和6,第三边的长是方程x2 - 6x + 8 = 0的根,则这个三角形的周长等于( )
A、13 B、11 C、11 或13 D、12或15
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区九年级10月调研数学试卷(解析版) 题型:选择题
已知⊙ 的直径为3cm,点
的直径为3cm,点 到圆心
到圆心 的距离
的距离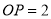 cm,则点
cm,则点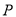 ( )
( )
A.在⊙ 外 B.在⊙
外 B.在⊙ 上 C.在⊙
上 C.在⊙ 内 D.不能确定
内 D.不能确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省徐州市九年级上学期第一次质检数学试卷(解析版) 题型:解答题
在等腰△ABC中,三边分别为a、b、c,其中a=5,若关于x的方程x2+(b+2)x+6-b=0有两个相等的实数根,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com