
(本题8分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.

(1)断⊿BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断。
(1)△BEC是直角三角形,理由见解析;
(2)四边形EFPH为矩形,证明见解析;
【解析】
试题分析:(1)由矩形性质得出CD=2,根据勾股定理求出CE和BE,求出CE2+BE2的值,求出BC2,根据勾股定理的逆定理求出即可;
(2)由矩形的性质和平行四边形的判定,推出平行四边形DEBP和AECP,推出EH∥FP,EF∥HP,推出平行四边形EFPH,根据矩形的判定推出即可;
试题解析:(1)△BEC是直角三角形,
理由是:∵矩形ABCD,
∴∠ADC=∠ABP=90°,AD=BC=5,AB=CD=2,
由勾股定理得:CE= ,
,
同理BE=2 ,
,
∴CE2+BE2=5+20=25,
∵BC2=52=25,
∴BE2+CE2=BC2,
∴∠BEC=90°,
∴△BEC是直角三角形.
(2)四边形EFPH为矩形,
∵矩形ABCD,
∴AD=BC,AD∥BC,
∵DE=BP,
∴四边形DEBP是平行四边形,
∴BE∥DP,
∵AD=BC,AD∥BC,DE=BP,
∴AE=CP,
∴四边形AECP是平行四边形,
∴AP∥CE,
∴四边形EFPH是平行四边形,
∵∠BEC=90°,
∴平行四边形EFPH是矩形.
考点:1、勾股定理及逆定理;2、矩形的性质和判定;3、平行四边形的性质和判定;4、三角形的面积
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性

科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值和抛物线与x轴的交点。
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y>0?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:选择题
关于x的一元二次方程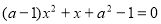 有一个根为0,则a的值是( )
有一个根为0,则a的值是( )
A、±1 B、-1 C、1 D、0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年天津市九年级上学期期中考试数学试卷(解析版) 题型:选择题
三角形两边长分别是8和6,第三边长是一元二次方程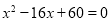 一个实数根,则该三角形的面积是( )
一个实数根,则该三角形的面积是( )
A.24 B.48 C.24或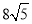 D.
D.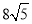
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:计算题
(6分)如图,矩形ABCD中,对角线AC和BD交于点O,M、N分别为OA、OD的中点。求证:BM=CN
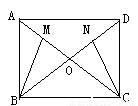
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省镇江市丹徒区九年级10月调研数学试卷(解析版) 题型:计算题
(8分)已知,如图1, 中,
中, ,
, 是平面内不与
是平面内不与 、
、 、
、 重合的任意一点,
重合的任意一点, ,
, .
.

(1)求证: ≌
≌ ;
;
(2)如图2,当点 是
是 的外接圆圆心时,请判断四边形
的外接圆圆心时,请判断四边形 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com