
抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值和抛物线与x轴的交点。
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y>0?
(1)m=3;抛物线与x轴交点坐标为(3,0),(-1,0).
(2)当x>1时,y的值随x的增大而减小
(3)当-1<x<3时,y>0.
【解析】
试题分析:(1)将点(0,3)代入抛物线的解析式中,即可求得m的值;令y=0,即可得出一个关于x的一元二次方程,方程的解就是抛物线与x轴交点的横坐标;
(2)求出抛物线的对称即可得到;
(3)由(1)中抛物线与x轴的交点以及抛物线的开口方向即可求得x的取值范围.
试题解析::(1)将(0,3)代入抛物线的解析式得:m=3.
∴抛物线的解析式为:y=-x2+2x+3,
令y=0,则有:-x2+2x+3=0,解得x1=3,x2=-1,
∴抛物线与x轴交点坐标为(3,0),(-1,0).
(2)抛物线y=-x2+2x+3的开口向下,对称轴为直线x= ,
,
∴当x>1时,y的值随x的增大而减小
(3)因为抛物线开口向下,所以当-1<x<3时,抛物线位于x轴上方,即y>0.
考点:1、待定系数法;2、抛物线与x轴的交点;3、抛物线的性质
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


科目:初中数学 来源:2014-2015学年黑龙江省大庆市九年级上学期期末检测数学试卷(解析版) 题型:填空题
如图,已知函数 和
和 的图象交于点P(-2,-5),则根据图象可得不等式
的图象交于点P(-2,-5),则根据图象可得不等式 的解集是_______________.
的解集是_______________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:解答题
(14分)如图,已知抛物线 与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线
与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线 .
.

(1)求抛物线的解析式;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:选择题
不解方程,判别一元二次方程 根的情况是( )
根的情况是( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.无法确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:选择题
抛物线 的顶点坐标是( )
的顶点坐标是( )
A.(1,3) B.(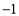 ,3) C.(1,
,3) C.(1,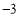 ) D.(
) D.( ,
,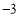 )
)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
如图,边长为1的正方形ABCO,以A为顶点,且经过点C的抛物线与对角线交于点D,则点D的坐标为 .
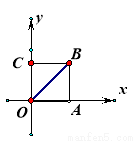
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为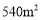 ,求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( )
,求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( )
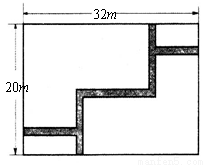
A.(20-x)(32-x)= 540
B.(20-x)(32-x)=100
C.(20+x)(32-x)=540
D.(20+x)(32-x)= 540
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(1)(4分)计算: .
.
(2)(5分)已知关于x的一元二次方程 有两个相等的实数根,求
有两个相等的实数根,求 的值。
的值。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期第一次月考数学试卷(解析版) 题型:解答题
(本题8分)如图,矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.

(1)断⊿BEC的形状,并说明理由;
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com