
(14分)如图,已知抛物线 与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线
与x轴交于A(-2,0)、B两点,与y轴交于C点,其对称轴为直线 .
.

(1)求抛物线的解析式;
(2)把线段AC沿x轴向右平移,设平移后A、C的对应点分别为A′、C′,当C′落在抛物线上时,求A′、C′的坐标;
(3)除(2)中的点A′、C′外,在x轴和抛物线上是否还分别存在点E、F,使得以A、C、E、F为顶点的四边形为平行四边形,若存在,求出E、F的坐标;若不存在,请说明理由.
(1) ;(2)A′(0,0),C′(2,4);(3)当点E为(
;(2)A′(0,0),C′(2,4);(3)当点E为( ,0),点F为(
,0),点F为(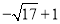 ,-4)或点E为(
,-4)或点E为( ,0),点F为(
,0),点F为(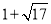 ,-4).
,-4).
【解析】
试题分析:(1)由A点的坐标和对称轴,根据待定系数法交点抛物线的解析式;
(2)根据平移性质及抛物线的对称性,求出A′、C′的坐标;
(3)以A、C、E、F为顶点的四边形为平行四边形,需要分两种情况讨论.
试题解析:(1)∵A(﹣2,0),对称轴为直线x=1.∴ ,
,
解得: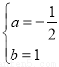 ,∴抛物线的解析式为:
,∴抛物线的解析式为: ;
;
(2)由抛物线 可知C(0,4),∵抛物线的对称轴为直线x=1,根据对称性,∴C′(2,4),∴A′(0,0);
可知C(0,4),∵抛物线的对称轴为直线x=1,根据对称性,∴C′(2,4),∴A′(0,0);
(3) 存在,共有两种情况:
①如图,四边形ACEF是平行四边形,过点F作FD⊥x轴,∴AF=CE,∠AEC=∠EAF,∠ADF=∠AOC=90°,∴∠DAF=∠CEO,∴△ADF≌△EOC,∴DF=CO=4,AD=EO,∴点F的纵坐标为-4,∵点F在抛物线 的图像上,即
的图像上,即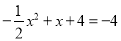 解得
解得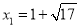 ,
, ,∴点F(
,∴点F(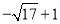 ,-4),
,-4),
∴DO= ,∵AO=2,∴AD=EO=DO-AO=
,∵AO=2,∴AD=EO=DO-AO= ,∴点E(
,∴点E(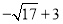 ,0),
,0),
所以点E的坐标为(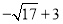 ,0),点F的坐标为(
,0),点F的坐标为(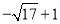 ,-4);
,-4);
②如图,四边形ACE′F′是平行四边形,过点F′作F′H⊥x轴,∴AC=E′F′,∠CAO=∠F′E′H,∠AOC=∠F′HE′=90°,∴△AOC≌△E′HF′,∴HF′=CO=4,AO=E′H,得点F′的纵坐标是-4,∵点F′在抛物线 的图像上,即
的图像上,即 ,解得
,解得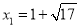 ,
, ,则点F′的坐标为(
,则点F′的坐标为( ,-4),∴EH=
,-4),∴EH= ,E′H=AO=2,∴OE′=
,E′H=AO=2,∴OE′= ,∴点E的坐标为(
,∴点E的坐标为( ,0),所以点E的坐标为(
,0),所以点E的坐标为( ,0),点F的坐标为(
,0),点F的坐标为( ,-4);
,-4);
综上可知,当点E(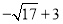 ,0),点F (
,0),点F (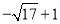 ,-4)或点E(
,-4)或点E( ,0),点F(
,0),点F( ,-4)时,以A、C、E、F为顶点的四边形为平行四边形.
,-4)时,以A、C、E、F为顶点的四边形为平行四边形.

考点:1.二次函数综合题;2.代数几何综合题.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


科目:初中数学 来源:2014-2015学年江苏省丹阳市十乡九年级下学期第一次联考数学试卷(解析版) 题型:选择题
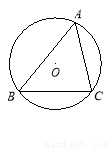
如图,△ABC内接于半径为5的⊙O,BC=8.则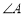 的正切值等于 ( )
的正切值等于 ( )
A.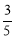 B.
B.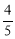 C.
C.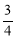 D.
D.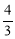
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省邯郸市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
二次函数 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
的大致图象如图所示,关于该二次函数,下列说法错误的是( )

A.函数有最小值
B.对称轴是直线x=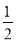
C.当x<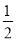 时,y随x的增大而减小
时,y随x的增大而减小
D.当 -1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省武夷山市九年级上学期期末质量监测数学试卷(解析版) 题型:解答题
(8分)参加一次商品交易会的两家公司之间都签订了一份合同,所有公司共签订了45份合同,共有多少家公司参加商品交易会?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值和抛物线与x轴的交点。
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y>0?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省九年级上学期第一次月考数学试卷(解析版) 题型:选择题
关于x的一元二次方程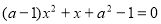 有一个根为0,则a的值是( )
有一个根为0,则a的值是( )
A、±1 B、-1 C、1 D、0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com