
����Ŀ��Ϊ�˹��������Լ��ˮ�����о���ʹ������ˮ�Ʒѷ�ʽʵʩ����ˮ�ۣ����������1����2�ֱ���С����С����С��С���ļ�2017�������ˮ���ͽ���ˮ�������
��1�������о�������ˮʵʩ����ˮ�۱������
���� | ÿ������ˮ���������ף� | ˮ�ۣ�����ˮ�����ѣ���Ԫ/�����ף� |
��һ���� | 0��m����m�� | a |
�ڶ����� | m��240����240�� | 4.40 |
�������� | 240���� | 7.85 |
��2���ĸ���ͥ2017�������ˮ���ͽ���ˮ�������
��ͥ | С�� | С�� | С�� | С�� |
��ˮ���������ף� | 50 | 100 | 200 | 220 |
ˮ�ѣ�Ԫ�� | 162.5 | 325 | 673 | 761 |
������ݱ�1����2�ṩ�����ݻش��������⣺
��1��д����1�е�a��m��ֵ��
��2��Сӱ��2017��ʹ������ˮ������ˮ��827Ԫ��������2017�������ˮ���Ƕ��������ף�
���𰸡���1��a��3.25��m��180����2������2017�������ˮ����235�����ף�
��������
��1������С����С����С��ҵ�����ˮ���ͽ���ˮ�������֪100��m��200���Ӷ����a��m��ֵ��
��2��������ˮ��Ϊ240������ʱ��������ˮ��849Ԫ����673��827��849���ɵ�����2017�������ˮ���ڵڶ����ݣ�������2017�������ˮ����x�����ף����ݹ�����ˮ��827Ԫ�г����̣���⼴�ɣ�
��1�������⣬�ɵ�a��![]() ��3.25��
��3.25��
����С�����ˮ200�����ף��ڵڶ����ݣ�������ˮ��673Ԫ��
�г����̣�3.25m+4.4��200��m����673��
���m��180��
��2��������ˮ��Ϊ240������ʱ��������ˮ�ѣ�3.25��180+4.4��240��180����849��Ԫ����
��673��827��849��
������2017�������ˮ���ڵڶ����ݣ�
������2017�������ˮ����x�����ף�
�������⣬��3.25��180+4.4��x��180����827��
���x��235��
������2017�������ˮ����235�����ף�


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ACB��90����AC��2��CB��4����PΪ�߶�CB��һ���㣬����AP����APC����APC������ֱ��AP�Գƣ����е�C�ĶԳƵ�Ϊ��C����ֱ��m����A��ƽ����CB
��1����ͼ�٣�����AB������C�����߶�AB��ʱ����BC���ij���
��2����ͼ�ڣ���PC��![]() BCʱ���ӳ�PC����ֱ��m�ڵ�D������ADC�������
BCʱ���ӳ�PC����ֱ��m�ڵ�D������ADC�������
��3���ڣ�2���������£�����BC����ֱ��д���߶�BC���ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
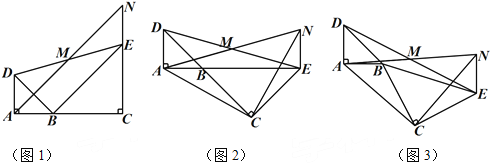
����Ŀ����ͼ1����֪��BAD����BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90������MΪDE���е㣮����E��ADƽ�е�ֱ�߽�����AM�ڵ�N��
��1����A��B��C������ͬһֱ����ʱ����ͼ1������֤��MΪAN���е㣻
��2����ͼ1����BCE�Ƶ�B��ת����A��B��E������ͬһֱ����ʱ����ͼ2������֤����CANΪ����ֱ�������Σ�
��3����ͼ1����BCE�Ƶ�B��ת��ͼ3��λ��ʱ��(2)�еĽ����Ƿ���Ȼ����������������֤��֮��������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��A��2��3����B��3��1����C����2����2�������ڸ���ϣ�
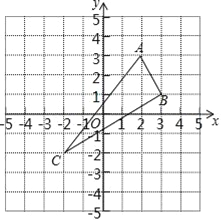
��1��������ABC����y��ԳƵġ�A1B1C1��
��2��ֱ��д����ABC����x��ԳƵġ�A2B2C2�ĸ������ꣻ
��3�������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����BAE+��AED=180������1=��2����ô��M=��N���������������̣�������գ���
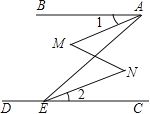
�⣺�ߡ�BAE+��AED=180������֪��
�� �� ��ͬ���ڽǻ�������ֱ��ƽ�У�
���BAE= ����ֱ��ƽ�У��ڴ�����ȣ�
���ߡ�1=��2
���BAE����1= ��
����MAE=
�� �� ���ڴ�����ȣ���ֱ��ƽ�У�
���M=��N����ֱ��ƽ�У��ڴ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����߲�Ʒ�ĸ���ֵ��ij��˾�ƻ����з�������1200���²�Ʒ���о��ӹ�����Ͷ���г������мס��������������߱��ӹ���������˾�ɳ������Ա�ֱ������������˽���������������Ϣ��
��Ϣһ�����������ӹ����������Ʒ���ҹ��������ӹ����������Ʒ����10�죻
��Ϣ�����ҹ���ÿ��ӹ��������Ǽ���ÿ��ӹ�������1.5����
����������Ϣ����ס�����������ÿ��ֱ��ܼӹ����ټ��²�Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��A��B�����������϶�Ӧ�����ֱ�Ϊ��12��4��
��1��ֱ��д��A��B����֮��ľ��룻
��2�����������ϴ���һ��P��ʹ��AP��![]() PB�����P��ʾ������
PB�����P��ʾ������

��3����ͼ2�����ж���P��Q������P�ӵ�A��������ÿ��5����λ���ȵ��ٶ������������˶���ͬʱ��Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ������������˶�������Q����ԭ��O��������ÿ��3����λ���ȵ��ٶ������������˶�����OP��4OQʱ���˶�ʱ��t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����![]() Ϊֱ��
Ϊֱ��![]() �ϵ㣬����
�ϵ㣬����![]() ������
������![]() ��
��![]() ����һֱ�����dz�(
����һֱ�����dz�(![]() )��ֱ�Ƕ�����ڵ�
)��ֱ�Ƕ�����ڵ�![]() ����һ��
����һ��![]() ������
������![]() �ϣ���һ��
�ϣ���һ��![]() ��
��![]() ����ֱ��
����ֱ��![]() ���Ϸ���
���Ϸ���
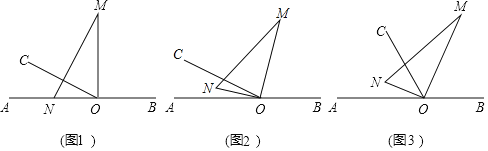
��1������ͼ��1���е����dz��Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶȣ���˳ʱ�뷽����ת
���ٶȣ���˳ʱ�뷽����ת![]() �룬��
�룬��![]() ǡ��ƽ��
ǡ��ƽ��![]() ʱ����ͼ��2����
ʱ����ͼ��2����
����![]() ֵ��
ֵ��
����˵����ʱ![]() ƽ��
ƽ��![]() ��
��
��2����ͼ��1���е����dz��Ƶ�![]() ˳ʱ����ת����
˳ʱ����ת����![]() ��
��![]() �� ��
�� ��![]() ��
��![]() �ڲ�ʱ������
�ڲ�ʱ������![]() ��
��![]() ��������ϵ��
��������ϵ��
��3������ͼ��1���е����dz��Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶ���˳ʱ�뷽����ת��ͬʱ������
���ٶ���˳ʱ�뷽����ת��ͬʱ������![]() Ҳ�Ƶ�
Ҳ�Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶ���˳ʱ�뷽����ת����ͼ��3������ô�����ʱ�䣬����
���ٶ���˳ʱ�뷽����ת����ͼ��3������ô�����ʱ�䣬����![]() ��һ��ƽ��
��һ��ƽ��![]() ����˵�����ɣ�
����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����Ϊ1��������ABCD�У�M��N�ֱ�ΪAD��BC���е㣬��C������MN�ϣ�����P���λ�ã��ۺ�ΪBQ������PQ����PQΪ�߳��������ε�������� �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com