
【题目】如图,面积为1的正方形ABCD中,M,N分别为AD、BC的中点,将C点折至MN上,落在P点的位置,折痕为BQ,连接PQ.以PQ为边长的正方形的面积等于 . 
【答案】![]()
【解析】解:由折法知PQ=QC,∠PBQ=∠QBC=30°.
在Rt△BCQ中,QC=BCtan30°=1× ![]() =
= ![]() ,
,
∴PQ= ![]() .
.
∴以PQ为边的正方形的面积为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了正方形的性质和翻折变换(折叠问题)的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,我市居民使用自来水计费方式实施阶梯水价,具体标准见表1,表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况.
表1:大连市居民自来水实施阶梯水价标准情况:
阶梯 | 每户年用水量(立方米) | 水价(含污水处理费)(元/立方米) |
第一阶梯 | 0~m(含m) | a |
第二阶梯 | m~240(含240) | 4.40 |
第三阶梯 | 240以上 | 7.85 |
表2:四个家庭2017年的年用水量和缴纳水费情况:
家庭 | 小明 | 小丽 | 小斌 | 小宇 |
用水量(立方米) | 50 | 100 | 200 | 220 |
水费(元) | 162.5 | 325 | 673 | 761 |
请你根据表1、表2提供的数据回答下列问题:
(1)写出表1中的a,m的值;
(2)小颖家2017年使用自来水共缴纳水费827元,则她家2017年的年用水量是多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
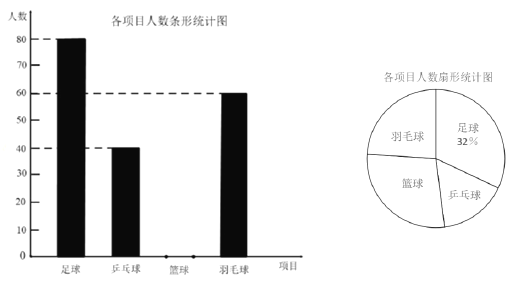
【题目】某学校举行“每天锻炼一小时,健康生活一辈子”为主题的体育活动,并开展了以下体育项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项。为了解选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)求选择篮球项目的人数在扇形统计图中所占的百分比?
(4)若该学校有1500人,请你估计该学校选择乒乓球项目的学生人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
类比定义:我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则等等.小学里,把分子比分母小的分数叫做真分数,类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.
拓展定义:
对于任何一个分式都可以化成整式与真分式的和的形式,
如:![]() ;
;
![]() .
.
理解定义:
(1)下列分式中,属于真分式的是:____属于假分式的是:_____(填序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
拓展应用:
(2)将分式![]() 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;
(3)将假分式![]() 化成整式与真分式的和的形式。
化成整式与真分式的和的形式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C为半圆上一点,N是线段BC上一点(不与B﹑C重合),过N作AB的垂线交AB于M,交AC的延长线于E,过C点作半圆O的切线交EM于F,若NC:CF=3:2,则sinB= .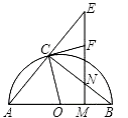
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: ![]() 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(i)解不等式(1),得;
(ii)解不等式(2),得;
(iii)把不等式(1)和(2)的解集在数轴上表示出来:![]()
(iv)原不等式的解集为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() ,
,![]() ;
;
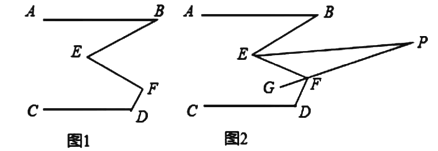
(1)若![]() ,则
,则![]() __________;
__________;
(2)请探索![]() 与
与![]() 之间满足的数量关系?说明理由;
之间满足的数量关系?说明理由;
(3)如图2,已知![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,反向延长
,反向延长![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点A为坐标原点,点B在x轴正半轴,点D在y轴正半轴,点C坐标为(6,m),点E是CD的中点,以CE为一边在矩形ABCD的内部作矩形CEFG,使点F在直线y=x上,交线段BC于点G,直线DG的函数表达式为y=- ![]() x+4,直线DG和AF交于点H.
x+4,直线DG和AF交于点H.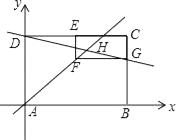
(1)求m的值;
(2)求点H的坐标;
(3)判断直线BE是否经过点H,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com