Question

【题目】解不等式组： 请结合题意填空，完成本题的解答：
（i）解不等式（1），得；
（ii）解不等式（2），得；
（iii）把不等式（1）和（2）的解集在数轴上表示出来：

（iv）原不等式的解集为： ．

Answer 1

【答案】x≤﹣3；x≥﹣5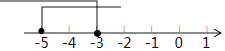； ；﹣5≤x≤﹣3
【解析】解：（i）解不等式（1），得x≤﹣3；

（ii）解不等式（2），得x≥﹣5；

（iii）把不等式（1）和（2）的解集在数轴上表示出来：

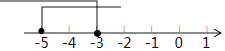
（iv）原不等式的解集为：﹣5≤x≤﹣3，

所以答案是：x≤﹣3；x≥﹣5；﹣5≤x≤﹣3．

【考点精析】关于本题考查的不等式的解集在数轴上的表示和一元一次不等式组的解法，需要了解不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈；解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能得出正确答案．