
【题目】二次函数y= ![]() (x﹣5)(x+m)(m是常数,m>0)的图象与x轴交于点A和点B(点A在点B的右侧)与y轴交于点C,连接AC.
(x﹣5)(x+m)(m是常数,m>0)的图象与x轴交于点A和点B(点A在点B的右侧)与y轴交于点C,连接AC.
(1)用含m的代数式表示点B和点C的坐标;
(2)垂直于x轴的直线l在点A与点B之间平行移动,且与抛物线和直线AC分别交于点M、N,设点M的横坐标为t,线段MN的长为p.
①当t=2时,求p的值;
②若m≤1,则当t为何值时,p取得最大值,并求出这个最大值.
【答案】
(1)解:令y=0,得 ![]() (x﹣5)(x+m)=0,
(x﹣5)(x+m)=0,
解得x1=5,x2=﹣m,
∵m>0,
∴﹣m<0,
∵点A在点B的右侧,
∴A(5,0),B(﹣m,0),
令x=0,得y=﹣ ![]() m,
m,
∴C(0,﹣ ![]() m)
m)
(2)解:①设AC的函数关系式为y=kx﹣ ![]() m,
m,
把A(5,0)代入y=kx﹣ ![]() m,解得k=
m,解得k= ![]() m,
m,
∴y= ![]() mx﹣
mx﹣ ![]() m,
m,
∵t=2,
∴点M的纵坐标为yM= ![]() (2﹣5)(2+m)=﹣
(2﹣5)(2+m)=﹣ ![]() (2+m),
(2+m),
点N的纵坐标为yN= ![]() m×2﹣
m×2﹣ ![]() m=﹣
m=﹣ ![]() m,
m,
∴p=yN﹣yM=﹣ ![]() m+
m+ ![]() (2+m)=3;
(2+m)=3;
②∵点M的横坐标为t,
∴点M的纵坐标为yM= ![]() (t﹣5)(t+m)=
(t﹣5)(t+m)= ![]() t2+
t2+ ![]() (m﹣5)t﹣
(m﹣5)t﹣ ![]() m,
m,
点N的纵坐标为yN= ![]() mt﹣
mt﹣ ![]() m,
m,
当0≤t≤5时,p=yN﹣yM=﹣ ![]() t2+
t2+ ![]() t=﹣
t=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
当t= ![]() 时,p取得最大值
时,p取得最大值 ![]() ,
,
当﹣m≤t<0时,p=yM﹣yN= ![]() t2﹣
t2﹣ ![]() t=
t= ![]() (t﹣
(t﹣ ![]() )2﹣
)2﹣ ![]() ,
,
此二次函数图象开口向上,对称轴为直线t= ![]() ,
,
∴在﹣m≤t<0时,p随t的增大而减少,
∴当t=﹣m时,p取得最大值为 ![]() m2+
m2+ ![]() m,
m,
设w= ![]() m2+
m2+ ![]() m,
m,
m=﹣ ![]() m为对称轴,
m为对称轴,
∴0<m≤1时,w的值随m的增大而增大,
∴m=1时,w最大值为3,
∵3< ![]() m,
m,
∴当t= ![]() 时,p取得最大值为
时,p取得最大值为 ![]() .
.
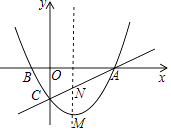
【解析】(1)纵坐标为0,横坐标为0,将其直接代入二次函数y= ![]() (x﹣5)(x+m)即可求得坐标.(2)①求p的值,通常利用表达式表示p,此时p恰为不含字母的式子.因为t=2,此时p=yN﹣yM,这里yM为点M的纵坐标,yN为点N的纵坐标;
(x﹣5)(x+m)即可求得坐标.(2)①求p的值,通常利用表达式表示p,此时p恰为不含字母的式子.因为t=2,此时p=yN﹣yM,这里yM为点M的纵坐标,yN为点N的纵坐标;
②求最值也要首先表示p,不过发现因为C为抛物线与直线的交点,在﹣m≤t≤0,p=yM﹣yN,当0≤t≤5时,p=yN﹣yM.如此要分开讨论最值,然后再综合在一起,讨论时不要遗漏题目中关于m的限制:0<m≤1.
【考点精析】关于本题考查的二次函数的性质,需要了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化,
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=20,b=12时的绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°,求∠B的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形.仔细观察图形可知:
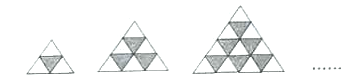
第1个图形中有1块黑色的瓷砖,可表示为![]() ;
;
第2个图形中有3块黑色的瓷砖,可表示为![]() ;
;
第3个图形中有6块黑色的瓷砖,可表示为![]() ;
;
则第![]() 个图形中有__________块黑色的瓷砖(
个图形中有__________块黑色的瓷砖(![]() 为正整数).
为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
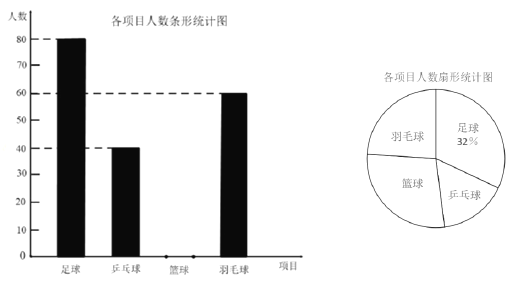
【题目】某学校举行“每天锻炼一小时,健康生活一辈子”为主题的体育活动,并开展了以下体育项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项。为了解选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
(1)这次活动一共调查了 名学生;
(2)补全条形统计图;
(3)求选择篮球项目的人数在扇形统计图中所占的百分比?
(4)若该学校有1500人,请你估计该学校选择乒乓球项目的学生人数约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点![]() 、
、![]() 、
、![]() 表示的数分别为4、0、
表示的数分别为4、0、![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒3个单位的速度沿数轴向左匀速运动.
点出发,以每秒3个单位的速度沿数轴向左匀速运动.
(1)当点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等时,点
的距离相等时,点![]() 在数轴上表示的数是 .
在数轴上表示的数是 .
(2)另一动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿数轴向左匀速运动,若点
出发,以每秒2个单位的速度沿数轴向左匀速运动,若点![]() 、
、![]() 同时出发,问点
同时出发,问点![]() 运动多长时间追上点
运动多长时间追上点![]() ?
?
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段
的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
类比定义:我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则等等.小学里,把分子比分母小的分数叫做真分数,类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.
拓展定义:
对于任何一个分式都可以化成整式与真分式的和的形式,
如:![]() ;
;
![]() .
.
理解定义:
(1)下列分式中,属于真分式的是:____属于假分式的是:_____(填序号)
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
拓展应用:
(2)将分式![]() 化成整式与真分式的和的形式;
化成整式与真分式的和的形式;
(3)将假分式![]() 化成整式与真分式的和的形式。
化成整式与真分式的和的形式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: ![]() 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(i)解不等式(1),得;
(ii)解不等式(2),得;
(iii)把不等式(1)和(2)的解集在数轴上表示出来:![]()
(iv)原不等式的解集为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把杜甫(绝句)整齐排列放在平面直角坐标系中:

(1)“东”、“窗”和“柳”的坐标依次是:______、______和________.;
(2)将第1行与第3行对调,再将第4列与第6列对调,“里”由开始的坐标________依次变换到:________和________;
(3)“门”开始的坐标是(1,1),使它的坐标到(3,2),应该哪两行对调,同时哪两列对调?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com