
【题目】如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化,
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=20,b=12时的绿化面积.

【答案】(1)(5a2+3ab)平方米;(2)2720平方米
【解析】
(1)根据割补法,用含有a,b的式子表示出整个长方形的面积,然后用含有a,b的式子表示出中间空白处正方形的面积,然后两者相减,即可求出绿化部分的面积.
(2)将a=20,b=12分别代入(1)问中求出的关系式即可解决.
解:(1)(3a+b)(2a+b)﹣(a+b)2=6a2+3ab+2ab+b2﹣(a2+2ab+b2)=6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2=5a2+3ab,
答:绿化的面积是(5a2+3ab)平方米;
(2)当a=20,b=12时
5a2+3ab=5×202+3×20×12=2000+720=2720,
答:当a=20,b=12时的绿化面积是2720平方米.


科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90o,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE,连接DE、DF、EF.

(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.

(1)在给定方格纸中画出平移后的△A′B′C′;
(2)画出AB边上的中线CD和BC边上的高线AE;
(3)线段AA′与线段BB′的关系是: ;
(4) 求四边形ACBB′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
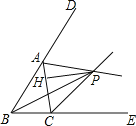
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
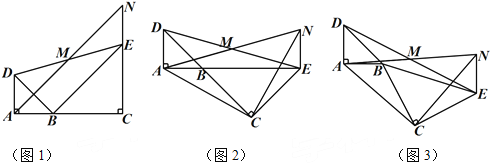
【题目】如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
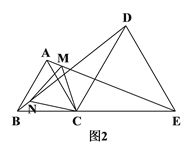
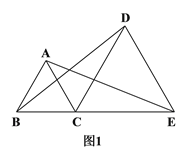
【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A(2,3),B(3,1),C(﹣2,﹣2)三点在格点上.
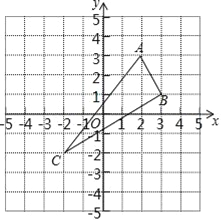
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)直接写出△ABC关于x轴对称的△A2B2C2的各点坐标;
(3)求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y= ![]() (x﹣5)(x+m)(m是常数,m>0)的图象与x轴交于点A和点B(点A在点B的右侧)与y轴交于点C,连接AC.
(x﹣5)(x+m)(m是常数,m>0)的图象与x轴交于点A和点B(点A在点B的右侧)与y轴交于点C,连接AC.
(1)用含m的代数式表示点B和点C的坐标;
(2)垂直于x轴的直线l在点A与点B之间平行移动,且与抛物线和直线AC分别交于点M、N,设点M的横坐标为t,线段MN的长为p.
①当t=2时,求p的值;
②若m≤1,则当t为何值时,p取得最大值,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com