Question

【题目】如图1，C是线段BE上一点，以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE，连结AE、BD．

（1）求证：BD=AE；

（2）如图2，若M、N分别是线段AE、BD上的点，且AM=BN，请判断△CMN的形状，并说明理由．

Answer 1

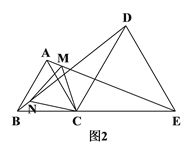
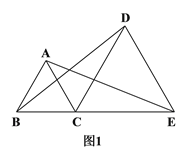
【答案】（1）证明见解析；（2）等边三角形，理由见解析.

【解析】试题分析：（1）由等边三角形的性质，可证明△DCB≌△ACE，可得到BD=AE；

（2）结合（1）中△DCB≌△ACE，可证明△ACM≌△BCN，进一步可得到∠MCN=60°且CM=CN，可判断△CMN为等边三角形．

试题解析：（1）∵△ABC、△DCE均是等边三角形，

∴AC=BC，DC=DE，∠ACB=∠DCE=60°，∴∠ACB+∠ACD=∠DCE+∠ACD，即∠BCD=∠ACE，

在△DCB和△ACE中，∵AC=BC，∠BCD =∠ACE， DC=DE，∴△DCB≌△ACE（SAS），∴BD=AE；

（2）△CMN为等边三角形，理由如下：由（1）可知：△ACE≌△DCB，

∴∠CAE=∠CDB，即∠CAM=∠CBN，

∵AC=BC，AM=BN，

在△ACM和△BCN中，∵AC=BC，∠CAM=∠CBN，AM=BN，∴△ACM≌△BCN（SAS），

∴CM=CN，∠ACM=∠BCN，

∵∠ACB=60°即∠BCN+∠ACN=60°，∴∠ACM+∠ACN=60°即∠MCN=60°，∴△CMN为等边三角形．