
【题目】某商家到梧州市一茶厂购买茶叶,购买茶叶数量为x千克(x>0),总费用为y元,现有两种购买方式. 方式一:若商家赞助厂家建设费11500元,则所购茶叶价格为130元/千克;(总费用=赞助厂家建设费+购买茶叶费)
方式二:总费用y(元)与购买茶叶数量x(千克)满足下列关系式:y= ![]() .
.
请回答下面问题:
(1)写出购买方式一的y与x的函数关系式;
(2)如果购买茶叶超过150千克,说明选择哪种方式购买更省钱;
(3)甲商家采用方式一购买,乙商家采用方式二购买,两商家共购买茶叶400千克,总费用共计74600元,求乙商家购买茶叶多少千克?
【答案】
(1)解:y=130x+11500
(2)解:∵x>150,
∴对于方式二有:y=150x+7500,
令150x+7500>130x+11500,
则x>200,
∴当150<x<200时,选择方式二购买更省钱;当x=200时,选择两种购买方式花费都一样;当x>200时,选择方式一购买更省钱
(3)解:设乙商家购买茶叶x千克,
若x≤150,则200x+130(400﹣x)+11500=74600,解得x=158 ![]() >150(不符合题意),
>150(不符合题意),
若x>150,则150x+7500+130(400﹣x)+11500=74600,解得x=180.
答:乙商家购买茶叶180千克
【解析】(1)根据方式一的总费用的组成列式即可;(2)判断出方式二的解析式,然后列不等式求出方式一比方式二费用大的x的值,再根据购买数量分别作出判断;(3)设乙商家购买茶叶x千克,然后分x≤150和x>150两种情况列出方程求解即可.


科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
 (3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标。
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
收费 方式 | 月使用费(元) | 包时上网 时间(h) | 超时费(元/min) |
A | 7 | 25 | 0.6 |
B | 10 | 50 | 0.8 |
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴已知xy=5,x+y=6,则x-y=______
⑵已知(2016-a)(2017-a)=5,(a-2016)2+(2017-a)2的值为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
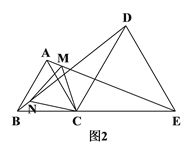
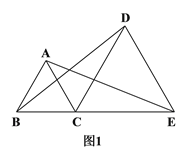
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(﹣2,﹣4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.
(1)求此抛物线的解析式;
(2)求点D的坐标;
(3)抛物线上是否存在点K,使得以AC为边的平行四边形ACKL的面积等于△ABC的面积?若存在,请直接写出点K的横坐标;若不存在,请说明理由.[提示:抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣ ![]() ,顶点坐标为(﹣
,顶点坐标为(﹣ ![]() ,
, ![]() )].
)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在方格纸中,
(1)请在方格纸上建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;
(2)把△ABC向右平移6个单位长度,再向上平移2个单位长度,画出平移后的图 形△A′B′C′;
(3)计算△A′B′C′的面积S .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com