
【题目】下面是由同一型号的黑白两种颜色的等边三角形瓷砖按一定规律铺设的图形.仔细观察图形可知:
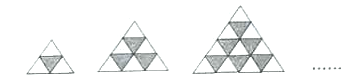
第1个图形中有1块黑色的瓷砖,可表示为![]() ;
;
第2个图形中有3块黑色的瓷砖,可表示为![]() ;
;
第3个图形中有6块黑色的瓷砖,可表示为![]() ;
;
则第![]() 个图形中有__________块黑色的瓷砖(
个图形中有__________块黑色的瓷砖(![]() 为正整数).
为正整数).
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
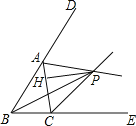
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() 为直线
为直线![]() 上点,过点
上点,过点![]() 作射线
作射线![]() ,
,![]() ,将一直角三角尺(
,将一直角三角尺(![]() )的直角顶点放在点
)的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 与
与![]() 都在直线
都在直线![]() 的上方.
的上方.
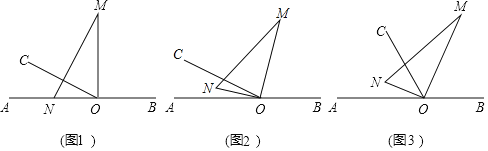
(1)若将图(1)中的三角尺绕点![]() 以每秒
以每秒![]() 的速度,沿顺时针方向旋转
的速度,沿顺时针方向旋转![]() 秒,当
秒,当![]() 恰好平分
恰好平分![]() 时,如图(2).
时,如图(2).
①求![]() 值;
值;
②试说明此时![]() 平分
平分![]() ;
;
(2)将图(1)中的三角尺绕点![]() 顺时针旋转,设
顺时针旋转,设![]() ,
,![]() , 当
, 当![]() 在
在![]() 内部时,试求
内部时,试求![]() 与
与![]() 的数量关系;
的数量关系;
(3)若将图(1)中的三角尺绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转的同时,射线
的速度沿顺时针方向旋转的同时,射线![]() 也绕点
也绕点![]() 以每秒
以每秒![]() 的速度沿顺时针方向旋转,如图(3),那么经过多长时间,射线
的速度沿顺时针方向旋转,如图(3),那么经过多长时间,射线![]() 第一次平分
第一次平分![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y= ![]() (x﹣5)(x+m)(m是常数,m>0)的图象与x轴交于点A和点B(点A在点B的右侧)与y轴交于点C,连接AC.
(x﹣5)(x+m)(m是常数,m>0)的图象与x轴交于点A和点B(点A在点B的右侧)与y轴交于点C,连接AC.
(1)用含m的代数式表示点B和点C的坐标;
(2)垂直于x轴的直线l在点A与点B之间平行移动,且与抛物线和直线AC分别交于点M、N,设点M的横坐标为t,线段MN的长为p.
①当t=2时,求p的值;
②若m≤1,则当t为何值时,p取得最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,现将正方形OABC绕点O顺时针旋转.
(1)如图①,当点A的对应的A′落在直线y=x上时,点A′的对应坐标为;点B的对应点B′的坐标为;
(2)旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N,当A点第一次落在直线y=x上时,停止旋转.
①如图2,在正方形OABC旋转过程中,线段AM,MN,NC三者满足什么样的数量关系?请说明理由;
②当AC∥MN时,求△MBN内切圆的半径(直接写出结果即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com