
分析 原式括号中两项通分并利用同分母分式的减法法则计算,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{x+3}{x-2}$÷($\frac{{x}^{2}-4}{x-2}$-$\frac{5}{x-2}$)
=$\frac{x+3}{x-2}$÷$\frac{{x}^{2}-9}{x-2}$
=$\frac{x+3}{x-2}$•$\frac{x-2}{(x+3)(x-3)}$
=$\frac{1}{x-3}$,
当x=3+$\sqrt{3}$时,原式=$\frac{1}{3+\sqrt{3}-3}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查分式的化简求值,根据分式的混合运算顺序和法则将原式化简是解题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
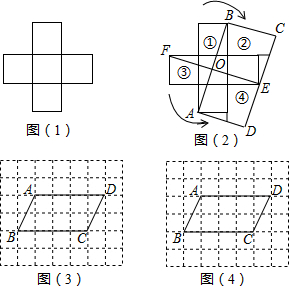
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.| 类别 | 时间t(小时) | 人数 |
| A | t≤0.5 | 5 |
| B | 0.5<t≤1 | 20 |
| C | 1<t≤1.5 | a |
| D | 1.5<t≤2 | 30 |
| E | t>2 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
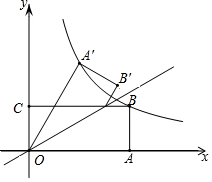 如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.
如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=$\frac{k}{x}$(k≠0)的图象恰好经过点A′,B,则k的值为$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).
抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线y=x-5上,与y轴相交于点D(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
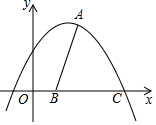 已知抛物线的解析式为y=-$\frac{1}{20}$x2+bx+5.
已知抛物线的解析式为y=-$\frac{1}{20}$x2+bx+5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com