

分析 (1)先根据角平分线的性质求出∠DBC、∠DCB与∠A的关系,再根据三角形内角和定理求解即可;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠A+∠ABC=∠ACE,∠D+∠DBC=∠DCE,再根据角平分线的定义可得∠DBC=$\frac{1}{2}$∠ABC,∠DCE=$\frac{1}{2}$∠ACE,然后整理可得∠D=$\frac{1}{2}$∠A;
(3)先根据外角平分线的性质求出∠DBC、∠DCB与∠A的关系,再由三角形内角和定理解答即可.
解答 解:(1)∵BD、CD是∠ABC和∠ACB的角平分线,
∴∠DBC=$\frac{1}{2}$∠ABC,∠DCB=$\frac{1}{2}$∠ACB,
∵∠ABC+∠ACB=180°-∠A,
∠BDC=180°-∠DBC-∠DCB=180°-$\frac{1}{2}$(∠ABC+∠ACB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A,
∴∠BDC=90°+$\frac{1}{2}$∠A=90°+$\frac{1}{2}$α;
(2)由三角形的外角性质,∠A+∠ABC=∠ACE,∠D+∠DBC=∠DCE,
∵∠ABC的平分线与∠ACB的外角平分线交于点D,
∴∠DBC=$\frac{1}{2}$∠ABC,∠DCE=$\frac{1}{2}$∠ACE,
∴$\frac{1}{2}$(∠A+∠ABC)=∠D+$\frac{1}{2}$∠ABC,
∴∠D=$\frac{1}{2}$∠A,
∵∠A=α,
∴∠D=$\frac{1}{2}α$;
(3)解:∵BD、CD是∠ABC和∠ACB外角的平分线,
∴∠CBD=$\frac{1}{2}$(∠A+∠ACB),∠BCD=$\frac{1}{2}$(∠A+∠ABC),
∵∠ABC+∠ACB=180°-∠A,
∠BDC=180°-∠CBD-∠BCD=180°-$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC)
=180°-$\frac{1}{2}$(2∠A+180°-∠A)=90°-$\frac{1}{2}$∠A.
即∠BDC=90°-$\frac{1}{2}$∠A=90°-$\frac{1}{2}α$.
点评 本题考查的是三角形外角的性质及三角形内角和定理:(1)三角形外角的性质:三角形的外角等于和它不相邻的两个内角的和;(2)三角形内角和定理:三角形的内角和为180°.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:选择题
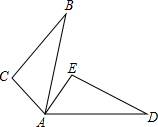 已知:如图,△ABC≌△ADE,AB与AD是对应边,AC与AE是对应边,若∠B=31°,∠C=95°,∠EAB=20°,则∠BAD等于( )
已知:如图,△ABC≌△ADE,AB与AD是对应边,AC与AE是对应边,若∠B=31°,∠C=95°,∠EAB=20°,则∠BAD等于( )| A. | 77° | B. | 74° | C. | 47° | D. | 44° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
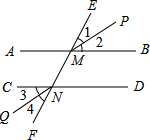 如图,下面四个条件中,请你以其中两个为已知条件,第三个作为结论,推出一个正确的命题.(只需写出一种情况)①AB∥CD;②∠1=∠4;③∠3=∠2;④MP∥NQ.
如图,下面四个条件中,请你以其中两个为已知条件,第三个作为结论,推出一个正确的命题.(只需写出一种情况)①AB∥CD;②∠1=∠4;③∠3=∠2;④MP∥NQ.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 只有平均数 | B. | 只有中位数 | ||
| C. | 只有众数 | D. | 平均数、中位数、众数均可 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≠0 | B. | a>-2且 a≠0 | C. | a>-2或 a≠0 | D. | a≥-2且 a≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2{b}^{2}}{a}$+8 | B. | 2009 | C. | 8 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com