
����Ŀ��ij�̳�����һ�ֵ���Ϊ40Ԫ����������Ե���50Ԫ���ۣ���ôÿ�¿��۳�500�����������۾��飬�ۼ�ÿ���1Ԫ����������Ӧ����10����
��1���������۵������Ԫ����ô����ÿ����������õ������� Ԫ����������ÿ�µ��������� �������ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2��8000Ԫ�Ƿ�Ϊÿ��������������������������ǣ���˵�����ɣ�������ǣ�������������ʱ������ۼ�Ӧ��Ϊ����Ԫ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�͡�DEF�У�AB=AC��DE=DF����A=��D.
��1����֤�� ![]() .
.
��2���ɣ�1���еĽ��ۿ�֪������������ABC�У������ǡ�A�Ĵ�Сȷ��ʱ�����ĶԱߣ����ױ�BC�����ڱߣ�����AB��AC���ı�ֵҲ��ȷ�������ǰ������ֵ����T(A)����
![]() ����T(60��)=1.
����T(60��)=1.
������̣�T(90��)= ________��T(120��)=_________�������ǵ��������εĶ��ǣ���T(��)��ȡֵ��Χ��_____________________��
��ѧ�����ã���ͼ2��Բ��ĸ�߳�Ϊ9������ֱ��PQ=8��һֻ���ϴӵ�������Բ�IJ������е���Q�����������е����·��������ȷ��0.1��.
���ο����ݣ�T(160��)��1.97��T(80��)��1.29��T(40��)��0.68��
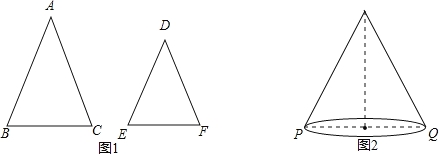
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P��������y=2��x��2��2�Գ����ϵ�һ�����㣬ֱ��x=tƽ��y�ᣬ�ֱ���y=x�������߽��ڵ�A��B������ABP���Ե�A���BΪֱ�Ƕ���ĵ���ֱ�������Σ�������������t��ֵ����t= ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������м�����������Ϊ�����εıߣ���1��8��15��17����2��5��12��13����3��12��15��20����4��7��24��25����������Ϊֱ�������ε����߳�����
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016���ʴ����ݲ�ҵ����������5��25����5��29���ڹ������У���չ����Ϊ��A�����ú���ᷢչ��B����ҵ��Ӧ�ã�C�����������ƣ�D����ȫ����˽������E��������������飬Ϊ�˽���ڶ�����������ע�������ij��������������ʾ����飬�������������Ƴ���������ͳ��ͼ�������������������ͳ��ͼ���ṩ����Ϣ������������⣺
��1��������������˶��������ڣ�
��2���벹ȫͳ��ͼ�����������ͳ��ͼ����D����ȫ����˽����������Ӧ������Բ�ĽǵĶ�����
��3������ر��������β����Ṳ������90000������ǰ���ιۣ�����ƹ�ע��E�������������������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ҫ˵��������������ʽ�Ĵ�����ͬ����������ͬ����Ǽ����⣬���Ծٵķ����ǣ� ����
A.2ab��3ab
B.2a2b��3ab2
C.2ab��2a2b2
D.2a3�ͩ�2a3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com