
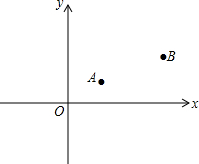 如图,已知A、B两村庄的坐标分别为A(2,2),B(7,4),一辆汽车在x轴上行驶,从原点O出发.
如图,已知A、B两村庄的坐标分别为A(2,2),B(7,4),一辆汽车在x轴上行驶,从原点O出发.分析 (1)根据垂线段的性质,可得答案;
(2)根据垂线段的性质,可得答案;
(3)根据线段垂直平分线的性质,可得B′,根据待定系数法,可得AB′,根据函数值,可得相应自变量的值,根据两点之间线段最短,可得答案;
(4)根据勾股定理,可得答案.
解答 解:(1)汽车行驶到(2,0)点时,离A村最近;
(2)汽车行驶到(7,0)点时,离B村最近;
(3)B′(7,-2),
AB′的解析式为y=-$\frac{4}{5}$x+$\frac{18}{5}$,
当y=0时,x=$\frac{9}{2}$,
汽车行驶到($\frac{9}{2}$,0)位置时,
如图: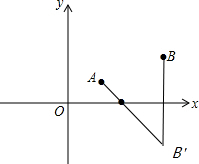
到A、B两村的距离的和最短请在图中标出位置;
(4)AB二点的距离$\sqrt{(7-2)^{2}+(4-2)^{2}}$=$\sqrt{29}$.
点评 本题考查了坐标确定位置,利用了垂线段的性质,勾股定理,线段垂直平分线的性质,线段的性质.


科目:初中数学 来源: 题型:解答题
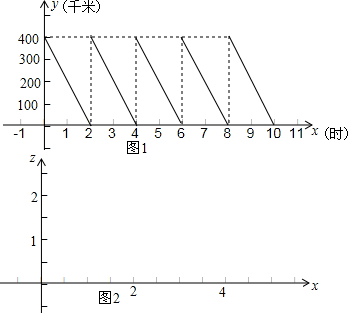 我们已经研究过函数的增减性(即单调性)、函数的对称性(即奇偶性)、函数的有界性,今天我们来研究一下函数的周期性.生活中有很多具有周期性的例子,如钟表的指针绕钟表圆心周而复始的旋转等,再如下面的例子:
我们已经研究过函数的增减性(即单调性)、函数的对称性(即奇偶性)、函数的有界性,今天我们来研究一下函数的周期性.生活中有很多具有周期性的例子,如钟表的指针绕钟表圆心周而复始的旋转等,再如下面的例子:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点B的坐标为(1,1),点E的坐标为($\frac{1+\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$).
如图,若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y=$\frac{1}{x}$(x>0)的图象上,则点B的坐标为(1,1),点E的坐标为($\frac{1+\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
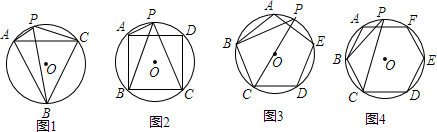
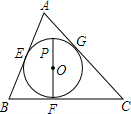 如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )
如图所示,⊙O是等边△ABC的内切圆,切点分别为E、F、G,P是$\widehat{EG}$上任意一点,则∠EPF的度数等于( )| A. | 120° | B. | 90° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
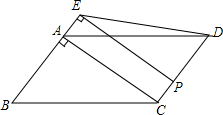 如图,在?ABCD中,在AB=3,BC=5,对角线AC⊥AB.点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度向终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连结PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).
如图,在?ABCD中,在AB=3,BC=5,对角线AC⊥AB.点P从点D出发,沿折线DC-CB以每秒1个单位长度的速度向终点B运动(不与点B、D重合),过点P作PE⊥AB,交射线BA于点E,连结PD、DE.设点P的运动时间为t(秒),△PDE与?ABCD重叠部分图形的面积为S(平方单位).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
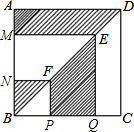 正方形ABCD的边长为2,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于2.
正方形ABCD的边长为2,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com