
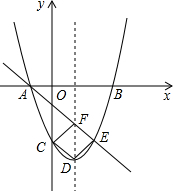
 ��ͼ�����κ���y=ax2+bx+c��ͼ����x���ཻ�ڵ�A��-1��0����B��3��0������y���ཻ�ڵ�C��0��-3����
��ͼ�����κ���y=ax2+bx+c��ͼ����x���ཻ�ڵ�A��-1��0����B��3��0������y���ཻ�ڵ�C��0��-3�������� ��1�����ô���ϵ�������ɽ�����⣮
��2�������ı���EFCD�������Σ���ͼ1�У�����CE��DF���ڵ�K�����E��F��D��C�ĵ����ֻ꣬Ҫ֤��DF��CE��DF=CE��KC=KE��KF=KD����֤����
��3����ͼ2�У�������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ����ݵ�P��������Ϊ2��-2�����ɽ�����⣮
��� �⣺��1����A��-1��0����B��3��0����C��0��-3������y=ax2+bx+c��$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=-3}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=-3}\end{array}\right.$��
�������ߵĽ���ʽΪy=x2-2x-3��
��2�������ı���EFCD�������Σ�
���ɣ���ͼ1�У�����CE��DF���ڵ�K��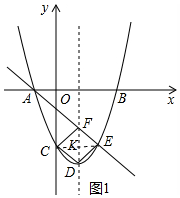
��y=��x-1��2-4��
�ඥ��D��1��4����
��C��E���ڶԳ���Գƣ�C��0��-3����
��E��2��-3����
��A��-1��0������ֱ��AE�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=-3}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$��
��ֱ��AE�Ľ���ʽΪy=-x-1��
��F��1��-2����
��CK=EK=1��FK=DK=1��
���ı���EFCD��ƽ���ı��Σ�
�֡�CE��DF��CE=DF��
���ı���EFCD�������Σ�
��3����ͼ2�У�������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�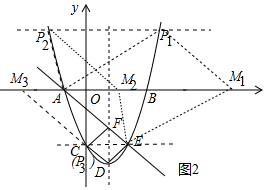
�������P��������Ϊ3��-3��
��y=3ʱ��x2-2x-3=3�����x=1��$\sqrt{7}$��
�ɵ�P1��1+$\sqrt{7}$��2����P2��1-$\sqrt{7}$��2����
��y=-2ʱ��x=0���ɵ�P3��0��-3����
����������P������Ϊ��1+$\sqrt{7}$��3����1-$\sqrt{7}$��3����0��-3��ʱ��������A��E��M��PΪ��������AEΪһ�ߵ�ƽ���ı��Σ�
���� ���⿼����κ����ۺ��⡢����ϵ������һ�κ�����Ӧ�á������ε��ж������ʡ�ƽ���ı��ε��ж������ʵ�֪ʶ������Ĺؼ���������ô���ϵ����ȷ����������ʽ��ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��������Ϊ��-3��2�� | B�� | �Գ���Ϊ��ֱ��x=-3 | ||
| C�� | ��x��3ʱy��x�������С | D�� | ��������Сֵ��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 5 | C�� | 25 | D�� | 29 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ��������ABC�У���C=90�㣬AB=10��AC=8����E��F�ֱ�ΪAC��AB���е㣬��EF=3��
��ͼ����ֱ��������ABC�У���C=90�㣬AB=10��AC=8����E��F�ֱ�ΪAC��AB���е㣬��EF=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com