
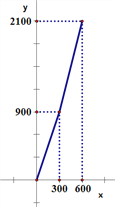
【题目】随着人民生活水平的提高,越来越多的家庭采取分户式采暖,降低采暖用气价格的呼声强烈.某市物价局对市区居民管道天然气阶梯价格制度的规定作出了调整,调整后的付款金额y(单位:元)与年用气量(单位:m3)之间的函数关系如图所示:
(1)宸宸家年用气量是270m3,求付款金额.
(2)皓皓家去年的付款金额是1300元,求去年的用气量.
【答案】(1)当![]() 时,y=3x,当x=270时,y=810;
时,y=3x,当x=270时,y=810;
(2)当900≤x≤2100时,y=4x-300,当y=1300时,x=400;
【解析】试题分析:(1)先根据图象得出分段函数的解析式,再把x=270带入求y值即可;
(2)令(1)中的解析式y=1300,解得相应x值即可.
试题解析:(1)当![]() 时,设y=kx,
时,设y=kx,
把(300,900)代入得:900=300k,
解得k=3,所以y=3x;
当![]() 时,设直线解析式为:y=kx+b,
时,设直线解析式为:y=kx+b,
把(300,900),(600,2100)代入得: ![]() ,
,
解得: ![]() ,所以直线解析式为:y=4x-300,
,所以直线解析式为:y=4x-300,
当x=270时,y=3×270=810(元)
答:付款金额为810元;
(2)当y=1300时,1300=4x-300,
解得x=400,
答:去年的用气量为400m3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道。有以下两个方案:
方案一:只取一个连接点P,使得像两个小区铺设的支管道总长度最短,在图中标出点P的位置,保留画图痕迹;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最短. 在途中标出M、N的位置,保留画图痕迹;
设方案一中铺设的支管道总长度为L1,方案二中铺设的支管道总长度为L2,则L1与L2的大小关系为:L1_______L2(填“>”、“<”或“=”)理由是____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在![]() 处,BC为折痕。
处,BC为折痕。
(1)图①中,若∠1=30°,求∠![]() 的度数;
的度数;
(2)如果又将活页的另一角斜折过去,使BD边与BA重合,折痕为BE,如图②所示,∠1=30°,求∠2以及∠![]() 的度数;
的度数;
(3)如果在图②中改变∠1的大小,则![]() 的位置也随之改变,那么问题(2)中∠
的位置也随之改变,那么问题(2)中∠![]() 的大小是否改变?请说明理由。
的大小是否改变?请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一条长为40cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于52cm2,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于48cm2吗?若能,求出两段铁丝的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.

(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.
①若BD=![]() ,求四边形BCDE的面积;
,求四边形BCDE的面积;
②若AB=3,AD=2,设CD2=x,EB2=y,求y与x之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
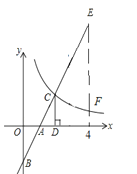
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②![]() ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房地产开发公司计划建![]() 、
、![]() 两种户型的住房共80套,该公司所筹资金不少于
两种户型的住房共80套,该公司所筹资金不少于![]() 万元,但不超过
万元,但不超过![]() 万元,且所筹资金全部用于建房,两种户型的建房的成本和售价如表:
万元,且所筹资金全部用于建房,两种户型的建房的成本和售价如表:
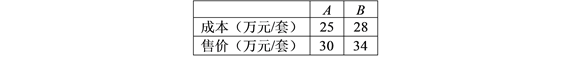
(![]() )该公司对这两种户型住房有哪几种方案?
)该公司对这两种户型住房有哪几种方案?
(![]() )该公司如何建房获利利润最大?
)该公司如何建房获利利润最大?
(![]() )根据市场调查,每套
)根据市场调查,每套![]() 型住房的售价不会改变,每套
型住房的售价不会改变,每套![]() 型住房的售价将会提高
型住房的售价将会提高![]() 万元
万元![]() ,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
,且所建的两种住房可全部售出,该公司又将如何建房获得利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差( | |
初中部 | a | 85 | b |
|
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差![]() ,并判断哪一个代表队选手成绩较为稳定.
,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com