
分析 (1)根据运算法则,即可解答;
(2)把g(g(x))=4x-1转化为g(g(x))=2(2x-$\frac{1}{3}$)-$\frac{1}{3}$,即可解答;
(3)把h(2x+1)=3x2+1转化为h(2x+1)=$\frac{3}{4}(2x+1)^{2}-\frac{3}{2}$(2x+1)+$\frac{7}{4}$,即可解答.
解答 解:(1)f(2)=9×22+3×2+6=48,f(-6)=9×(-6)2+3×(-6)+6=312.
(2)g(g(x))=2(2x-$\frac{1}{3}$)-$\frac{1}{3}$,
∴g(x)=2x-$\frac{1}{3}$.
(3)∵h(2x+1)=$\frac{3}{4}(2x+1)^{2}-\frac{3}{2}$(2x+1)+$\frac{7}{4}$,
∴h(x)=$\frac{3}{4}{x}^{2}-\frac{3}{2}x+\frac{7}{4}$.
点评 本题考查了代数式求值,解决本题的关键是明确运算法则.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
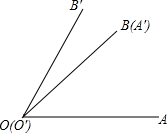 如图,将∠A′O′B′的顶点0′和∠A0B的顶点0重合,边0′A与边0B重合,并使两个角的另一边0A和0′B′分别在重合边0B(O′A)的两旁,这时它们不重合的两边组成∠AOB′.那么∠AOB′,∠A0B与∠A′0′B′之间有什么数量关系?
如图,将∠A′O′B′的顶点0′和∠A0B的顶点0重合,边0′A与边0B重合,并使两个角的另一边0A和0′B′分别在重合边0B(O′A)的两旁,这时它们不重合的两边组成∠AOB′.那么∠AOB′,∠A0B与∠A′0′B′之间有什么数量关系?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
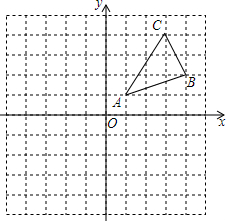 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有理数可分为整数、分数和0 | |
| B. | 如果两个数的绝对值相等,那么它们互为相反数 | |
| C. | 边长为a的正方形面积是5,则a是无理数 | |
| D. | 互为相反数的两个数的商是-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com