
| A. | $\frac{41}{9}$ | B. | $\frac{41}{8}$ | C. | $\frac{41}{6}$ | D. | $\frac{41}{7}$ |
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
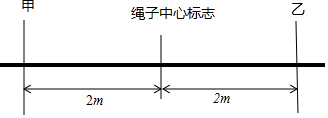 如图,是甲、乙两队同学进行拔河比赛的示意图,绳子的中心标志先向甲方移动0.8m,再向乙方移动1.2m.相持一段时间后,先向乙方移动0.5m,再向甲方移动1.8m,然后向乙方移动0.3m,最后向甲方移动1.6m.若根据规定,绳子的中心标志物从中点处向哪一队的方向移动超过2m.则该队获胜那么现在哪一个队取得了胜利?请通过计算说明你的判断.
如图,是甲、乙两队同学进行拔河比赛的示意图,绳子的中心标志先向甲方移动0.8m,再向乙方移动1.2m.相持一段时间后,先向乙方移动0.5m,再向甲方移动1.8m,然后向乙方移动0.3m,最后向甲方移动1.6m.若根据规定,绳子的中心标志物从中点处向哪一队的方向移动超过2m.则该队获胜那么现在哪一个队取得了胜利?请通过计算说明你的判断.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{{x}^{2}y}$ | C. | $\sqrt{8x}$ | D. | $\sqrt{{x}^{2}+{y}^{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,B,点C在x轴上,P在线段AB上(含端点),CP的最小值是2.直接写出C点的横坐标的取值范围.
直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$与x轴,y轴分别交于点A,B,点C在x轴上,P在线段AB上(含端点),CP的最小值是2.直接写出C点的横坐标的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com