Question

【题目】在平面直角坐标系中，已知A（1，1）、B（3，5），要在x轴上找一点P，使得△PAB的周长最小，则点P的坐标为 ．

Answer 1

【答案】（0，2）．

【解析】

试题解析：∵线段AB的长度是确定的，

∴△PAB的周长最小就是PA+PB的值最小，

∵3＜5，

∴点P在y轴上，

如图1，作点A关于y轴的对称点A′，连接A′B交y轴于点P，

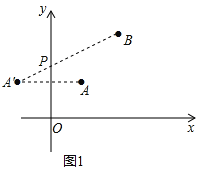
∵A（1，1），

∴A′（-1，1），

设直线A′B的解析式为y=kx+b（k≠0），

∴，解得，

∴直线A′B的解析式为y=x+2，

当x=0时，y=2，

∴P（0，2）．

A′B=；

如图2，作点A关于x轴的对称点A′，连接A′B交y轴于点P，

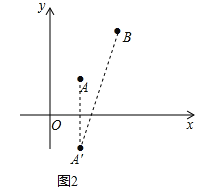
∵A（1，1），

∴A′（1，-1），

设直线A′B的解析式为y=kx+b（k≠0），

∴，解得，

∴直线A′B的解析式为y=3x-4，

当y=0时，x=，

∴P（，0）．

A′B=．

∵＜．

故点P的坐标为（0，2）．