
 如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$.
如图已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…An′作x轴的垂线交二次函数y=$\frac{1}{2}$x2(x>0)的图象于点P1,P2,P3,…Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,则S3=$\frac{5}{4}$,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn==$\frac{2n-1}{4}$. 分析 先根据二次函数图象上点的坐标特征,求出P1(1,$\frac{1}{2}$),则根据三角形面积公式计算出S1=$\frac{1}{4}$,同样可得S2=$\frac{3}{4}$;S3=$\frac{5}{4}$,S4=$\frac{7}{4}$,所有相应三角形的面积等于分母为4,分子为奇数的分式,从而得到
Sn=$\frac{2n-1}{4}$.
解答 解:当x=1时,y=$\frac{1}{2}$x2=$\frac{1}{2}$,则P1(1,$\frac{1}{2}$),所以S1=$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$;
当x=2时,y=$\frac{1}{2}$x2=2,则P2(2,2),所以S2=$\frac{1}{2}$×1×(2-$\frac{1}{2}$)=$\frac{3}{4}$;
当x=3时,y=$\frac{1}{2}$x2=$\frac{9}{2}$,则P3(3,$\frac{9}{2}$),所以S3=$\frac{1}{2}$×1×($\frac{9}{2}$-2)=$\frac{5}{4}$,
同样方法可得S4=$\frac{7}{4}$,
所以Sn=$\frac{2n-1}{4}$.
故答案为$\frac{5}{4}$,$\frac{2n-1}{4}$.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了三角形面积公式.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
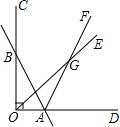 已知如图,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
已知如图,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
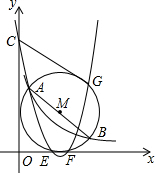 如图,已知点A(n,6),B(6,m)在双曲线y=$\frac{6}{x}$的图象上,以AB为直径的eM与x轴交于点E(3,0)和点F,抛物线y=ax2+bx+12(a≠0)的图象经过点A、E、F.
如图,已知点A(n,6),B(6,m)在双曲线y=$\frac{6}{x}$的图象上,以AB为直径的eM与x轴交于点E(3,0)和点F,抛物线y=ax2+bx+12(a≠0)的图象经过点A、E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
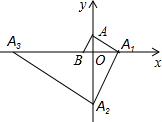 如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为(-31008,0),.
如图,在平面直角坐标系中,点A(0,$\sqrt{3}$)、B(-1,0),过点A作AB的垂线交x轴于点A1,过点A1作AA1的垂线交y轴于点A2,过点A2作A1A2的垂线交x轴于点A3…按此规律继续作下去,直至得到点A2015为止,则点A2015坐标为(-31008,0),.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com