
设 都是实数,且
都是实数,且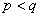 .我们规定:满足不等式
.我们规定:满足不等式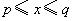 的实数
的实数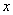 的所有取值的全体叫做闭区间,表示为
的所有取值的全体叫做闭区间,表示为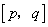 .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量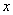 与函数值
与函数值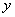 满足:当
满足:当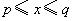 时,有
时,有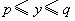 ,我们就称此函数是闭区间
,我们就称此函数是闭区间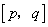 上的“闭函数”.
上的“闭函数”.
(1)反比例函数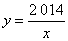 是闭区间
是闭区间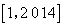 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数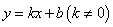 是闭区间
是闭区间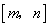 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若实数c,d满足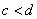 ,且
,且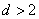 ,当二次函数
,当二次函数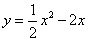 是闭区间
是闭区间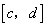 上的“闭函数”时,求
上的“闭函数”时,求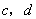 的值.
的值.
解:(1)是;
由函数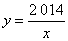 的图象可知,当
的图象可知,当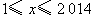 时,函数值
时,函数值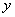 随着自变量
随着自变量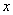 的增大而减少,而当
的增大而减少,而当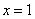 时,
时, ;
; 时,
时,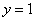 ,故也有
,故也有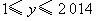 ,
,
所以,函数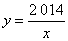 是闭区间
是闭区间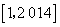 上的“闭函数”.
上的“闭函数”.
(2)因为一次函数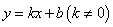 是闭区间
是闭区间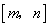 上的“闭函数”,所以根据一次函数的图象与性质,必有:
上的“闭函数”,所以根据一次函数的图象与性质,必有:
①当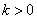 时,
时, ,解之得
,解之得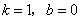 .
.
∴一次函数的解析式为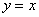 .
.
②当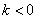 时,
时,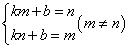 ,解之得
,解之得 .
.
∴一次函数的解析式为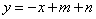 .…
.…
故一次函数的解析式为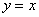 或
或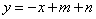 .
.
(3)由于函数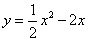 的图象开口向上,且对称轴为
的图象开口向上,且对称轴为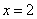 ,顶点为
,顶点为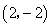 ,由题意根据图象,分以下两种情况讨论:
,由题意根据图象,分以下两种情况讨论:
①当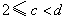 时,必有
时,必有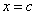 时,
时,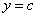 且
且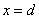 时,
时,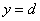 ,
,
即方程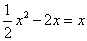 必有两个不等实数根,解得
必有两个不等实数根,解得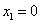 ,
,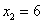 .
.
而0,6分布在2的两边,这与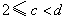 矛盾,舍去;
矛盾,舍去;
②当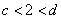 时,必有函数值
时,必有函数值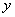 的最小值为
的最小值为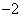 ,
,
由于此二次函数是闭区间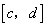 上的“闭函数”,故必有
上的“闭函数”,故必有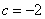 ,
,
从而有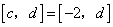 ,而当
,而当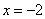 时,
时,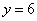 ,即得点
,即得点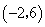 ;
;
又点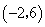 关于对称轴
关于对称轴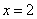 的对称点为
的对称点为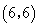 ,
,
由“闭函数”的定义可知必有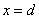 时,
时,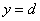 ,即
,即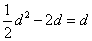 ,解得
,解得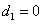 ,
,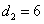 .
.
故可得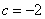 ,
,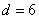 符合题意.
符合题意.
综上所述,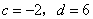 为所求的实数.
为所求的实数.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
由平谷统计局2013年12月发布的数据可知,我区的旅游业蓬勃发展,以下是根据近几年我区旅游业相关数据绘制统计图的一部分:
|
|
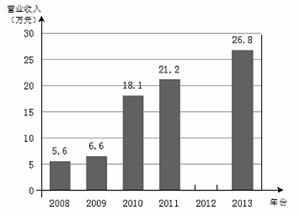
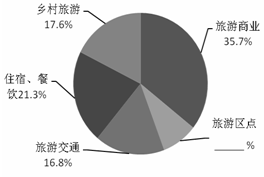
请你根据以上信息解答下列问题:
(1)计算2012年平谷区旅游区点营业收入占全区旅游营业收入的百分比,并补全扇形统计图;
(2)2012年旅游区点的收入为2.1万元,请你计算2012年平谷区旅游营业收入,并补全条形统计图 (结果保留一位小数) ;
(3)如果今年我区的旅游营业收入继续保持2013年的增长趋势,请你预测我区今年的旅游营业收入 (结果保留一位小数) .
查看答案和解析>>
科目:初中数学 来源: 题型:
以下统计图、表描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、下旬)日人均阅读时间的情况:
活动上旬频数分布直方图 活动中旬频数分布表
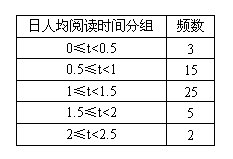
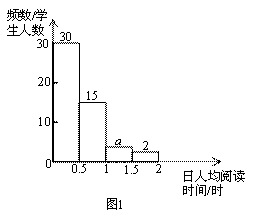
活动下旬频数分布扇形图
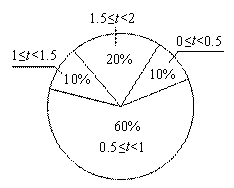
图2
(1)从以上统计图、表可知,九年级(1)班共有学生多少人?
(2)求出图1中a的值;
(3)从活动上旬和中旬的统计图、表判断,在这次读书月活动中,该班学生每日阅读时间
(填“普遍增加了”或“普遍减少了”);
(4)通过这次读书月活动,如果该班学生初步形成了良好的每日阅读习惯,参照以上统计图、表中的数据,至读书月活动结束时,该班学生日人均阅读时间在0.5~1小时的人数比活动开展初期增加了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
在一次数学游戏中,老师在 三个盘子里分别放了一些糖果,糖果数依次为
三个盘子里分别放了一些糖果,糖果数依次为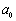 ,
,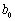 ,
,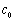 ,记为
,记为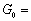 (
(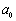 ,
,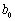 ,
,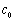 ). 游戏规则如下: 若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿
). 游戏规则如下: 若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿 出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作. 若三个盘子中的糖果数都相同,游戏结束.
出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作. 若三个盘子中的糖果数都相同,游戏结束. 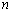 次操作后的糖果数记为
次操作后的糖果数记为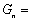 (
( ,
,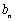 ,
, ).
).
(1)若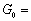 (4,7
(4,7 ,10),则第_______次操作后游戏结束;
,10),则第_______次操作后游戏结束;
(2)小明发现:若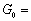 (4,8,18),则游戏永远无法结束,那么
(4,8,18),则游戏永远无法结束,那么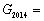 ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.以下是相关的统计图、表:

| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
(1)请根据所给信息补全扇形统计图;
(2)请你根据“2013年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重
污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2013年机动车保有量已突破520万辆,请你通过计算,估计2013年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com