Question

5．如图，点C在以AB为直径的半圆上，AB=8，∠ABC=30°，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F，下列结论：①CE=CF；②线段EF的最小值为2$\sqrt{3}$；③当AD=2时，EF与半圆相切，其中正确结论的序号是①③．

Answer 1

分析 ①由点E与点D关于AC对称可得CE=CD，再根据DF⊥DE即可证到CE=CF．
②根据“点到直线之间，垂线段最短”可得CD⊥AB时CD最小，由于EF=2CD，求出CD的最小值就可求出EF的最小值．
③连接OC，易证△AOC是等边三角形，AD=OD，根据等腰三角形的“三线合一”可求出∠ACD，进而可求出∠ECO=90°，从而得到EF与半圆相切．

解答 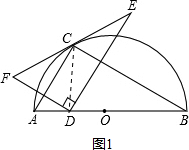解：①连接CD，如图1所示．
∵点E与点D关于AC对称，
∴CE=CD．
∴∠E=∠CDE．
∵DF⊥DE，
∴∠EDF=90°．
∴∠E+∠F=90°，∠CDE+∠CDF=90°．
∴∠F=∠CDF．
∴CD=CF．
∴CE=CD=CF．
∴结论“CE=CF”正确．
②当CD⊥AB时，如图2所示．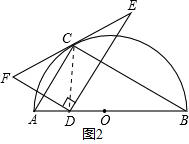
∵AB是半圆的直径，
∴∠ACB=90°．
∵AB=8，∠CBA=30°，
∴∠CAB=60°，AC=4，BC=4$\sqrt{3}$．
∵CD⊥AB，∠CBA=30°，
∴CD=$\frac{1}{2}$BC=2$\sqrt{3}$．
根据“点到直线之间，垂线段最短”可得：
点D在线段AB上运动时，CD的最小值为2$\sqrt{3}$．
∵CE=CD=CF，
∴EF=2CD．
∴线段EF的最小值为4$\sqrt{3}$．
∴结论“线段EF的最小值为2$\sqrt{3}$”错误．
③当AD=2时，连接OC，如图3所示．
∵OA=OC，∠CAB=60°，
∴△OAC是等边三角形．
∴CA=CO，∠ACO=60°．
∵AO=4，AD=2，
∴DO=2．
∴AD=DO．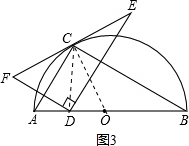
∴∠ACD=∠OCD=30°．
∵点E与点D关于AC对称，
∴∠ECA=∠DCA．
∴∠ECA=30°．
∴∠ECO=90°．
∴OC⊥EF．
∵EF经过半径OC的外端，且OC⊥EF，
∴EF与半圆相切．
∴结论“EF与半圆相切”正确；
故答案为：①③

点评 本题考查了等边三角形的判定与性质、切线的判定、轴对称的性质、垂线段最短等知识，关键是根据轴对称的性质和等边三角形的判定与性质进行分析．