练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

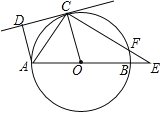
    如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E是AB延长线上一点，CE交⊙O于点F，连接OC、AC．

    （1）求证：AC平分∠DAO．

    （2）若∠DAO=105°，∠E=30°

    ①求∠OCE的度数；

    ②若⊙O的半径为2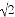，求线段EF的长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版九年级数学上册_第六章_反比例函数_单元检测试卷 题型：解答题

    如图所示，在平面直角坐标系中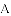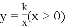，是反比例函数图象上一点；作垂直轴于点，垂直轴于点，正方形的面积为．

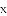
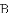
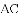
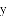
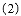
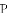
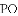
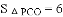    求该反比例函数的解析式；

    若点在反比例函数的图象上，连、且．求点的坐标．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级数学_上册_第四章_几何图形初步_单元检测试卷 题型：单选题

    下列各直线的表示法中，正确的是（ ）．

    A、直线A B、直线AB C、直线ab D、直线Ab

    查看答案和解析>>

    科目：初中数学 来源：人教版数学九年级（下） 第27章 《相似》 压轴专题综合练习 题型：解答题

    小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试.

    （1）如图①，垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A′B，D′C的长度和为6cm.那么灯泡离地面的高度为 .

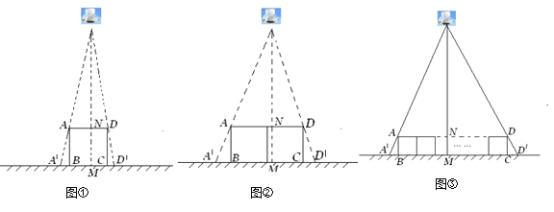    （2）不改变①中灯泡的高度，将两个边长为30cm的正方形框架按图②摆放，请计算此时横向影子A′B，D′C的长度和为多少？

    （3）有n个边长为a的正方形按图③摆放，测得横向影子A′B，D′C的长度和为b,求灯泡离地面的距离.（写出解题过程，结果用含a,b,n的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源：人教版数学九年级（下） 第27章 《相似》 压轴专题综合练习 题型：解答题

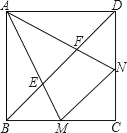
    已知：如图边长为2的正方形ABCD中，∠MAN的两边分别交BC、CD边于M、N两点，且∠MAN＝45°

    ①求证：MN＝BM+DN；

    ②若AM、AN交对角线BD于E、F两点．设BF＝y，DE＝x，求y与x的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源：2018-2019学年度人教版数学九年级上册 第24章《圆》单元测试卷 题型：解答题

    如果圆锥底面的周长是20π，侧面展开后所得扇形的圆心角为120°，求该圆锥的侧面积．

    查看答案和解析>>

    科目：初中数学 来源：2018-2019学年度人教版数学九年级上册 第24章《圆》单元测试卷 题型：单选题

    如图，在平面直角坐标系中，⊙P的圆心坐标是(3，a)(a＞3)，半径为3，函数y＝x的图象被⊙P截得的弦AB的长为4，则a的值是(　　)

    A. 4 B. 3＋ C. 3 D. 3＋

    查看答案和解析>>

    科目：初中数学 来源：2019届第一学期北师大版九年级数学上册综合检测试卷（全册） 题型：填空题

    已知图中的曲线是反比例函数（为常数）图象的一支．

    这个反比例函数图象的另一支在第________象限，常数的取值范围是________．

    若该函数的图象任取一点，过点作轴的垂线，垂足为，当的面积为时，求反比例函数的解析式．

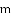
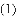
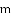
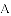
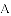
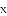
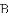
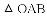
    查看答案和解析>>

    科目：初中数学 来源：北师大九年级数学上册综合检测试卷（全册） 题型：单选题

    在一个暗箱里放有个除颜色外其它完全相同的球，这个球中红球有个．每次将球搅拌均匀后，任意摸出一个球记下颜色再放回暗箱．通过大量重复摸球实验后发现，摸到红球的频率稳定在，那么可以推算出大约是（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案