练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

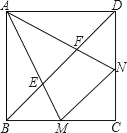
    已知：如图边长为2的正方形ABCD中，∠MAN的两边分别交BC、CD边于M、N两点，且∠MAN＝45°

    ①求证：MN＝BM+DN；

    ②若AM、AN交对角线BD于E、F两点．设BF＝y，DE＝x，求y与x的函数关系式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学上册_第六章_数据的收集与整理_单元检测试j题 题型：单选题

    名学生分别购买如下尺码的鞋子：，，，，，，，，．（单位：），这组数据中鞋店老板最关心的是（ ）

    A. 平均数 B. 中位数 C. 众数 D. 方差

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级数学_上册_第四章_几何图形初步_单元检测试卷 题型：填空题

    如果点，，在一条直线上，线段，线段，则、两点间的距离是________．

    查看答案和解析>>

    科目：初中数学 来源：人教版数学九年级（下） 第27章 《相似》 压轴专题综合练习 题型：解答题

    如图，在Rt△ABC中，∠C=90°，Rt△BAP中，∠BAP=90°，已知∠CBO=∠ABP，BP交AC于点O，E为AC上一点，且AE=OC．

    （1）求证：AP=AO；

    （2）求证：PE⊥AO；

    （3）当AE=AC，AB=10时，求线段BO的长度．

    查看答案和解析>>

    科目：初中数学 来源：人教版数学九年级（下） 第27章 《相似》 压轴专题综合练习 题型：解答题

    操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的圆形纸片进行如下设计：

    说明：方案一：图形中的圆过点A、B、C；

    方案二：直角三角形的两直角边与展开图左下角的正方形边重合，斜边经过两个正方形的顶点.

    纸片利用率=×100%

    发现：（1）方案一中的点A、B恰好为该圆一直径的两个端点．

    你认为小明的这个发现是否正确，请说明理由．

    （2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．

    请帮忙计算方案二的利用率，并写出求解过程．

    探究：

    （3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．

    查看答案和解析>>

    科目：初中数学 来源：2018-2019学年度人教版数学九年级上册 第24章《圆》单元测试卷 题型：解答题

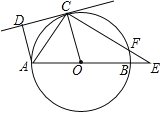
    如图，已知：AB是⊙O的直径，点C在⊙O上，CD是⊙O的切线，AD⊥CD于点D，E是AB延长线上一点，CE交⊙O于点F，连接OC、AC．

    （1）求证：AC平分∠DAO．

    （2）若∠DAO=105°，∠E=30°

    ①求∠OCE的度数；

    ②若⊙O的半径为2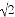，求线段EF的长．

    查看答案和解析>>

    科目：初中数学 来源：2018-2019学年度人教版数学九年级上册 第24章《圆》单元测试卷 题型：填空题

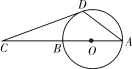
    如图所示，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C＝20°，则∠CDA＝___.

    查看答案和解析>>

    科目：初中数学 来源：2019届第一学期北师大版九年级数学上册综合检测试卷（全册） 题型：解答题

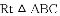
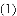
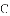
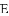
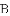
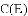
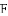
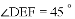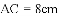
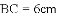
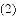
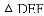
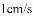
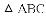
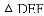
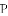
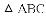
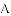
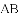
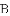
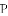
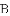
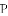
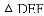
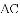
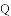
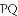
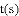
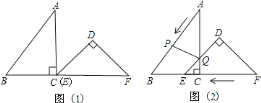
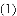
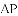
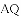
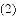
    把和按如图摆放（点与重合），点、、在同一条直线上．已知：，，，，．如图，从图的位置出发，以的速度沿向匀速移动，在移动的同时，点从的顶点出发，以的速度沿向点匀速移动；当点移动到点时，点停止移动，也随之停止移动．与交于点，连接，设移动时间为．

    用含的代数式表示线段和的长，并写出的取值范围；

    当为何值时，是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源：北师大九年级数学上册综合检测试卷（全册） 题型：填空题

    在比例尺为的地图上，量得甲、乙两地的距离是，则甲、乙两地的实际距离为________千米．

    查看答案和解析>>

    同步练习册答案