操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的圆形纸片进行如下设计：
说明：方案一：图形中的圆过点A、B、C；
方案二：直角三角形的两直角边与展开图左下角的正方形边重合，斜边经过两个正方形的顶点.
纸片利用率=
×100%
发现：（1）方案一中的点A、B恰好为该圆一直径的两个端点．
你认为小明的这个发现是否正确，请说明理由．
（2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．
请帮忙计算方案二的利用率，并写出求解过程．
探究：
（3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．
科目：初中数学 来源：北师大版七年级数学上册_第六章_数据的收集与整理_单元检测试j题 题型：单选题
中国总人口约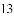
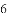
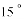，那么以下结论正确的是（ ）
A. 受中等教育的人口约占总人口的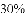
C. 受中等教育的人数大于五千万 D. 受中等教育的人数小于五百万
查看答案和解析>>
科目：初中数学 来源：人教版数学九年级（下） 第27章 《相似》 压轴专题综合练习 题型：解答题
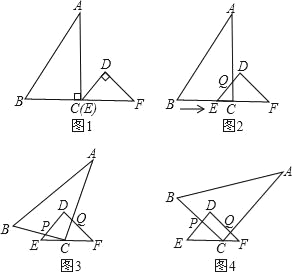
已知：RT△ABC与RT△DEF中，∠ACB＝∠EDF＝90°，∠DEF＝45°，EF＝8cm，AC＝16cm，BC＝12cm．现将RT△ABC和RT△DEF按图1的方式摆放，使点C与点E重合，点B、C（E）、F在同一条直线上，并按如下方式运动．
运动一：如图2，△ABC从图1的位置出发，以1cm/s的速度沿EF方向向右匀速运动，DE与AC相交于点Q，当点Q与点D重合时暂停运动；
运动二：在运动一的基础上，如图3，RT△ABC绕着点C顺时针旋转，CA与DF交于点Q，CB与DE交于点P，此时点Q在DF上匀速运动，速度为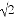
cm/s，当QC⊥DF时暂停旋转；
运动三：在运动二的基础上，如图4，RT△ABC以1cm/s的速度沿EF向终点F匀速运动，直到点C与点F重合时为止．
设运动时间为t（s），中间的暂停不计时，
解答下列问题
（1）在RT△ABC从运动一到最后运动三结束时，整个过程共耗时 s；
（2）在整个运动过程中，设RT△ABC与RT△DEF的重叠部分的面积为S（cm2），求S与t之间的函数关系式，并直接写出自变量t的取值范围；
（3）在整个运动过程中，是否存在某一时刻，点Q正好在线段AB的中垂线上，若存在，求出此时t的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源：人教版数学九年级（下） 第27章 《相似》 压轴专题综合练习 题型：解答题
如图，在△ABC中，点D、E、F分别在AB、BC、AC上，且∠ADF+∠DEC=180°，∠AFE=∠BDE．
（1）如图1，当DE=DF时，图1中是否存在于AB相等的线段？若存在，请找出并加以证明．若不存在说明理由．
（2）如图2，当DE=kDF（其中0<k<1）时，若∠A=90°，AF=m，求BD的长（用含k，m的式子表示）．
查看答案和解析>>
科目：初中数学 来源：人教版数学九年级（下） 第27章 《相似》 压轴专题综合练习 题型：解答题
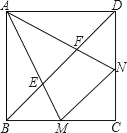
已知：如图边长为2的正方形ABCD中，∠MAN的两边分别交BC、CD边于M、N两点，且∠MAN＝45°
①求证：MN＝BM+DN；
②若AM、AN交对角线BD于E、F两点．设BF＝y，DE＝x，求y与x的函数关系式．
查看答案和解析>>
科目：初中数学 来源：2018-2019学年度人教版数学九年级上册 第24章《圆》单元测试卷 题型：解答题
如图，已知P是⊙O外一点，PO交圆O于点C，OC=CP=2，弦AB⊥OC，劣弧AB的度数为120°，连接PB．
（1）求BC的长；
（2）求证：PB是⊙O的切线．
查看答案和解析>>
科目：初中数学 来源：2018-2019学年度人教版数学九年级上册 第24章《圆》单元测试卷 题型：单选题
如图，在⊙O中，AC∥OB，∠BAO＝25°，则∠BOC的度数为( )
A. 25° B. 50° C. 60° D. 80°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
（配方法）；