
【题目】如图,在Rt直角△ABC中,∠BAC=90°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,则下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是_______________.

【答案】①②③
【解析】
根据等腰直角三角形的性质可得∠CAD=∠B=45°,根据同角的余角相等求出∠ADF=∠BDE,然后利用“角边角”证明△BDE和△ADF全等,判断出③正确;根据全等三角形对应边相等可得DE=DF、BE=AF,从而得到△DEF是等腰直角三角形,判断出①正确;再求出AE=CF,判断出②正确;根据BE+CF=AF+AE,利用三角形的任意两边之和大于第三边可得BE+CF>EF,判断出④错误.
解:∵∠B=45°,AB=AC,
∴△ABC是等腰直角三角形,
∵点D为BC中点,
∴AD=CD=BD,AD⊥BC,∠CAD=45°,
∴∠CAD=∠B,
∵∠MDN是直角,
∴∠ADF+∠ADE=90°,
∵∠BDE+∠ADE=∠ADB=90°,
∴∠ADF=∠BDE,
在△BDE和△ADF中,
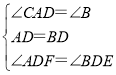 ,
,
∴△BDE≌△ADF(ASA),
故③正确;
∴DE=DF、BE=AF,
∴△DEF是等腰直角三角形,
故①正确;
∵AE=AB-BE,CF=AC-AF,
∴AE=CF,
故②正确;
∵BE+CF=AF+AE
∴BE+CF>EF,
故④错误;
综上所述,正确的结论有①②③.


科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系xoy中,点A、B分别在x、y轴的正半轴上,将线段AB绕点B顺时针旋转90°,点A的对应点为点C.

(1)若A(6,0),B(0,4),求点C的坐标;
(2)以B为直角顶点,以AB和OB为直角边分别在第一、二象限作等腰Rt△ABD和等腰Rt△OBE,连DE交y轴于点M,当点A和点B分别在x、y轴的正半轴上运动时,判断并证明AO与MB的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一个三角形中,其中有一个内角是另外一个内角的一半,则这样的三角形叫做“半角三角形”. 例如:等腰直角三角形就是“半角三角形”.在钝角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 交
交![]() 边于点
边于点![]() .点
.点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(1)若![]() ,点
,点![]() 在
在![]() 延长线上.
延长线上.
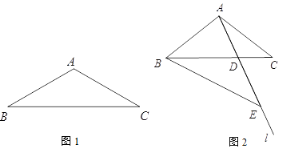
① 当![]() ,点
,点![]() 恰好为
恰好为![]() 中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
② 如图2,若![]() ,图中是否存在“半角三角形”(△
,图中是否存在“半角三角形”(△![]() 除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
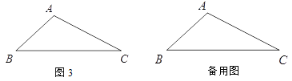
(2)如图3,若![]() ,保持
,保持![]() 的度数与(1)中②的结论相同,请直接写出
的度数与(1)中②的结论相同,请直接写出![]() ,
,![]() ,
,![]() 满足的数量关系:______.
满足的数量关系:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点且
上一点且![]() ,过点
,过点![]() 画线段
画线段![]() ,使点
,使点![]() 在
在![]() 的边上且点
的边上且点![]() ,
,![]() 与
与![]() 的一个顶点组成的小三角形与
的一个顶点组成的小三角形与![]() 相似,则满足条件的线段
相似,则满足条件的线段![]() 的长度分别为________.
的长度分别为________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数.
(2)求证:M是BE的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,若点P与△ABC三个顶点中的任意两个顶点连接形成的三角形都是等腰三角形,则称点P是△ABC的巧妙点.
(1)如图1,求作△ABC的巧妙点P(尺规作图,不写作法,保留作图痕迹).

(2)如图2,在△ABC中,∠A=80°,AB=AC,求作△ABC的所有巧妙点P (尺规作图,不写作法,保留作图痕迹),并直接写出∠BPC的度数是 .

(3)等边三角形的巧妙点的个数有( )
A.2 B.6 C.10 D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选2名同学打第一场比赛,求下列事件的概率。
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.

(1)操作:
过点A作AD⊥![]() 于点D,过点B作BE⊥
于点D,过点B作BE⊥![]() 于点E.求证:△CAD≌△BCE.
于点E.求证:△CAD≌△BCE.
(2)模型应用:
①如图2,在直角坐标系中,直线![]() :
:![]() 与y轴交于点A,与x轴交于点B,将直线
与y轴交于点A,与x轴交于点B,将直线![]() 绕着点A顺时针旋转45°得到直线
绕着点A顺时针旋转45°得到直线![]() .求直线
.求直线![]() 的函数表达式.
的函数表达式.
②如图3,在直角坐标系中,点B(4,3),作BA⊥y轴于点A,作BC⊥x轴于点C,P是直线BC上的一个动点,点Q(a,5a﹣2)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com