
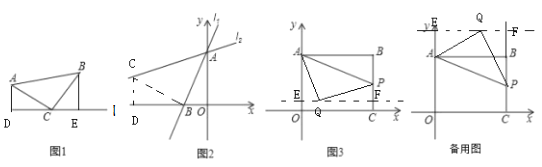
【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.

(1)操作:
过点A作AD⊥![]() 于点D,过点B作BE⊥
于点D,过点B作BE⊥![]() 于点E.求证:△CAD≌△BCE.
于点E.求证:△CAD≌△BCE.
(2)模型应用:
①如图2,在直角坐标系中,直线![]() :
:![]() 与y轴交于点A,与x轴交于点B,将直线
与y轴交于点A,与x轴交于点B,将直线![]() 绕着点A顺时针旋转45°得到直线
绕着点A顺时针旋转45°得到直线![]() .求直线
.求直线![]() 的函数表达式.
的函数表达式.
②如图3,在直角坐标系中,点B(4,3),作BA⊥y轴于点A,作BC⊥x轴于点C,P是直线BC上的一个动点,点Q(a,5a﹣2)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
【答案】(1)详见解析;(2)![]() (3)
(3)![]() 或
或![]() .
.
【解析】
(1)根据AAS即可证明△DAC≌△ECB;
(2)过点B作BC⊥BA,交直线l2于点C,过点C作CD⊥x轴于点D.根据![]() 得到AO=3,OB=1,根据△DCB≌△OBA可得点C的坐标为(-4,1),再根据待定系数法即可求解;
得到AO=3,OB=1,根据△DCB≌△OBA可得点C的坐标为(-4,1),再根据待定系数法即可求解;
(3)根据题意分两种情况分别作图即可求解.
(1)∵∠ACB=90°,
∴∠ACD+∠BCE=90°
∵AD⊥l,BE⊥l,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=90° ,
∴∠DAC=∠ECB
∵在△DAC和△ECB中,∠ADC=∠CEB,∠DAC=∠ECB,AC=CB
∴△DAC≌△ECB(AAS)
(2)过点B作BC⊥BA,交直线l2于点C,过点C作CD⊥x轴于点D.
由直线![]() :
:![]() 与y轴交于点A,与x轴交于点B,
与y轴交于点A,与x轴交于点B,
可求点A坐标为(0,3),点B坐标为(-1,0),
∴AO=3,OB=1.
由△DCB≌△OBA可得,DC=OB=1,DB=OA=3,
∴点C的坐标为(-4,1)
设直线m的解析式为:y=kx+b,把(0,3),(-4,1)代入,
求得![]() .
.
(3)如图3,由△AEQ≌△QFP可得AE=QF,3-(5a-2)=4-a,
求得![]() .
.
如备用图,由△AEQ≌△QFP可得AE=QF,(5a-2)-3=4-a,
求得![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt直角△ABC中,∠BAC=90°,AB=AC,点D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,则下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )

A. ac>0 B. 当x>0时,y随x的增大而减小
C. 2a﹣b=0 D. 方程ax2+bx+c=0的两根是x1=﹣1,x2=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八![]() 班组织了一次经典朗读比赛,甲、乙两队各
班组织了一次经典朗读比赛,甲、乙两队各![]() 人的比赛成绩如下表(
人的比赛成绩如下表(![]() 分制):
分制):
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
①甲队成绩的中位数是________分,乙队成绩的众数是________分;
②计算乙队的平均成绩和方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小军和小明玩一种抽卡片游戏,他们拿了八张扑克牌,将数字为![]() 、
、![]() 、
、![]() 、
、![]() 的四张牌给小军,将数字为
的四张牌给小军,将数字为![]() 、
、![]() 、
、![]() 、
、![]() 的四张牌给小明,并按如下游戏规则进行:小军和小明各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,若和为偶数,小军赢,若和为奇数,则小明赢.
的四张牌给小明,并按如下游戏规则进行:小军和小明各自的四张牌中随机抽出一张,然后将抽出的两张牌数字相加,若和为偶数,小军赢,若和为奇数,则小明赢.
![]() 请用树状图或列表法求小军获胜的概率.
请用树状图或列表法求小军获胜的概率.
![]() 这个游戏公平吗?请说明理由.
这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一根水平放置的圆柱形输水管道的横截面如图所示,其中有水部分水面宽![]() 米,最深处水深
米,最深处水深![]() 米,则此输水管道的直径等于( )
米,则此输水管道的直径等于( )
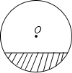
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 观察被开方数a的小数点与算术平方根![]() 的小数点的移动规律:
的小数点的移动规律:
a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| 0.01 | x | 1 | y | 100 |
填空:x= _______, y=______.
(2)根据你发现的规律填空:
①已知![]() ≈1.414,则
≈1.414,则![]() =________,
=________,![]() =_______;
=_______;
②![]() = 0.274,记
= 0.274,记![]() 的整数部分为x,则
的整数部分为x,则![]() =___________.
=___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com