
【题目】如图,已知抛物线C1:y=a(x+2)2﹣5的顶点为P,与x轴相较于A,B两点(点A在点B的左侧),且点B的坐标为(1,0)
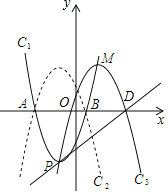
(1)求抛物线C1的函数解析式;
(2)如图,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,抛物线C3的顶点为M,当点P,M关于点O成中心对称时.①求点M的坐标;②求抛物线C3的解析式;
(3)在(2)的条件下,设抛物线C3与x轴的正半轴交于点D,在直线PD的上方的抛物线C3上,是否存在点Q使得△PDQ的面积最大?若存在,求出当点Q的横坐标为何值时△PDQ面积最大,若不存在请说明理由.
【答案】(1)抛物线C1的表达式为:y=![]() (x+2)2﹣5;
(x+2)2﹣5;
(2)①点M(2,5);②抛物线C3表达式为:y=﹣![]() (x﹣2)2+5;
(x﹣2)2+5;
(3)S有最大值,此时x=![]() ;Q的横坐标为
;Q的横坐标为![]() .
.
【解析】
(1)将点B的坐标代入抛物线C1的表达式并解得:a=![]() ,即可求解;
,即可求解;
(2)点P(2,5),则点M(2,5),则抛物线C3表达式中的a值为![]() ,点M(2,5),即可求解;
,点M(2,5),即可求解;
(3)△PDQ的面积S=![]() ×QH×(xD﹣xP)=
×QH×(xD﹣xP)=![]() (5+2)[﹣
(5+2)[﹣![]() (x﹣2)2+5﹣
(x﹣2)2+5﹣![]() x+
x+![]() ]=﹣
]=﹣![]() x2+
x2+![]() x+
x+![]() ,即可求解.
,即可求解.
解:(1)将点B的坐标代入抛物线C1的表达式并解得:a=![]() ,
,
故抛物线C1的表达式为:y=![]() (x+2)2﹣5;
(x+2)2﹣5;
(2)①∵点P(﹣2,﹣5),则点M(2,5);
②抛物线C3表达式中的a值为﹣![]() ,点M(2,5),
,点M(2,5),
故抛物线C3表达式为:y=﹣![]() (x﹣2)2+5;
(x﹣2)2+5;
(![]() (x﹣2)2+5,令y=0,则x=﹣1或5,故点D(5,0),
(x﹣2)2+5,令y=0,则x=﹣1或5,故点D(5,0),
设PD直线为y=kx+b(k≠0)
将点P(﹣2,﹣5)、D(5,0)的坐标代入一次函数表达式得
![]()
解得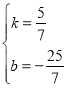 :
:
∴直线PD的表达式为:y=![]() x﹣
x﹣![]() ,
,
过点Q作y轴的平行线交直线PD于点H,
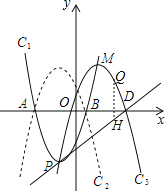
设点Q[x,﹣![]() (x﹣2)2+5],则点H(x,
(x﹣2)2+5],则点H(x,![]() x﹣
x﹣![]() ),
),
∴△PDQ的面积S=![]() ×QH×(xD﹣xP)
×QH×(xD﹣xP)
=![]() (5+2)[﹣
(5+2)[﹣![]() (x﹣2)2+5﹣
(x﹣2)2+5﹣![]() x+
x+![]() ]
]
=﹣![]() x2+
x2+![]() x+
x+![]() ,
,
∵﹣![]() <0,
<0,
∴S有最大值,此时x=![]() ;
;
Q的横坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为

A.(﹣1,![]() ) B.(﹣1,
) B.(﹣1,![]() )或(﹣2,0) C.(
)或(﹣2,0) C.(![]() ,﹣1)或(0,﹣2) D.(
,﹣1)或(0,﹣2) D.(![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计).若长方形纸板边长分别为40cm和30cm,且折成的长方体盒子表面积是950cm2,此时长方体盒子的体积为_____cm3.
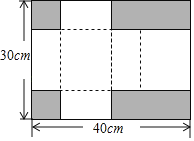
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且![]() ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②
,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;②![]() 的周长为
的周长为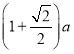 ;③
;③![]() ;④
;④![]() 的面积的最大值
的面积的最大值![]() .其中正确的结论是____.(填写所有正确结论的序号)
.其中正确的结论是____.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OC=2OB则下列结论:①abc<0;②a+b+c>0;③ac﹣2b+4=0;④OAOB=![]() ,其中正确的结论有( )
,其中正确的结论有( )
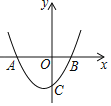
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )
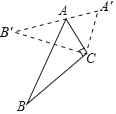
A. 65°B. 60°C. 50°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
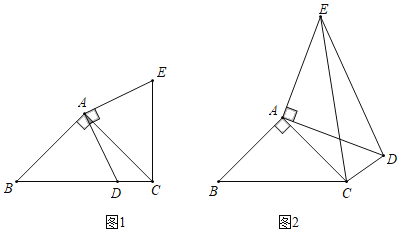
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC.
(1)如图1,通过图形旋转的性质可知AD=_____,∠DAE=_____度.
(解决问题)
(2)如图1,证明BC=DC+EC;
(拓展延伸)
如图2,在△ABC中,∠BAC=90°,AB=AC,D为△ABC外一点,且∠ADC=45°,仍将线段AD绕点A逆时针旋转90°得到AE,连接EC,ED.
(3)若AD=6,CD=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PE⊥PA,PE交OC的延长线于点E.
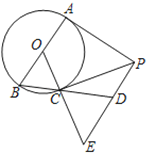
(1)求证:OE=PE;
(2)连接BC并延长交PE于点D,PA=AB,且CE=9,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
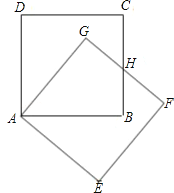
【题目】把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com