
���Ķ�����ͼ1����P��x��y����ƽ��ֱ�������У�����P��PA��x�ᣬ����ΪA������P�ƴ���A˳ʱ����ת�Ǧ���0�㣼����90�㣩�õ���Ӧ��P�䣬���dzƵ�P����P����˶�Ϊ��б���˶������磺��P��0��2����б30���˶���Ķ�Ӧ��ΪP�䣨1��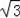
 ����
����
ͼ��E��ƽ��ֱ������ϵ�У�ͼ��E�ϵ����е㶼����б���˶���õ�ͼ��E�䣬�������˶���Ϊͼ��E����б���˶���

����
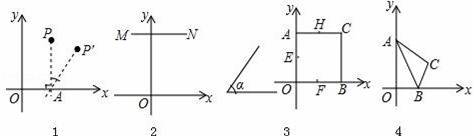
��1����Q��1��2����б60���˶���Ķ�Ӧ��Q�������Ϊ��������������
��2����ͼ2��ƽ����x����߶�MN��б���˶���õ���Ӧ�߶�M��N�䣬M��N����MNƽ���������˵�����ɣ�
Ӧ�ã���1����ͼ3��������AOBC��б���˶���������е�E��F��G��H�Ķ�Ӧ��E�䣬F�䣬G�䣬H�乹�ɵ��ı�����ʲô�����ı��Σ���������������
��2����ͼ4����֪��A��0��4����B��2��0����C��3��2��������ABC��б���˶����ܲ��ܵõ�Rt��A��B��C�䣬�ҡ�A��C��B��Ϊֱ�ǣ����е�A�䣬B�䣬C��Ϊ��A��B��C�Ķ�Ӧ�㣮�����cos����ֵ��
��
�����㡿���α任�ۺ��⣮
�����������⣺
��1��������Ŀ�гƵ�P��P����˶�Ϊ����˶��Ķ�������Q������ꣻ
��2��������Ŀ��ͼ��E������˶��Ķ�������ж�M��N����MN�Ĺ�ϵ��
Ӧ�ã�
��1���ο����⣨2���ɵã�������AOBC��ת���γ����Σ����ε��ı��е���ɵ��ı����Ǿ��Σ�
��2�������A��B��=4=OA�䣬�������Ǻ������cos����ֵ��
����𡿽⣺��1����ͼ1��
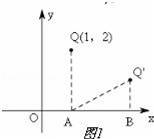

����Q��QA��x�ᣬ����ΪA������תQ����x��Ĵ��ߣ�����ΪB��
��Rt��ABQ���У���Q��AB=30�㣬BQ��=1��
�ɹ��ɶ�����AB=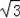
 ��
��
��OB=1+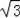
 ��
��
��Q���������1+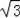
 ��1�����ʴ�Ϊ����1+
��1�����ʴ�Ϊ����1+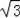
 ��1����
��1����
��2��M��N����MNƽ������ȣ�
�������£�
��ͼ2��


�ֱ����M��N��MA��x���ڵ�A��NB��x���ڵ�B��
��MN��AB����MN=AB��
�ɶ����֪��M��A��N��B��M��A=N��B��
���ı�M��ABN����ƽ���ı��Σ�
��M��N���AB��M��N��=AB��
��M��N����MNƽ������ȣ�
Ӧ�ã���1�������⣨2���ɵã�������AOBC��ת���γ����Σ�
���ε��ı��е���ɵ��ı����Ǿ��Σ�
�ʴ�Ϊ�����Σ�
��2���ܣ�cos��=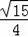
 ��
��
��ͼ3��
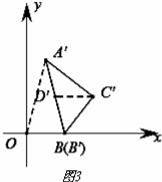

��AB���е�ΪD��
��D��������1��2����
��CD��x�ᣬ��CD=2��
��D���Ӧ��D����A��B���е㣬C��D��=2��
��C��D��=
 A��B�䣬
A��B�䣬
��A��B��=4=OA�䣬
�ߡϦ�=
 ��OA��B�䣬
��OA��B�䣬
��cos��=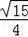
 ��
��
�������������Ǽ��α任�ۺ��⣬��Ҫ�����˹��ɶ�����ƽ���ı��ε����ʺ��ж������Σ������Σ����ε����ʺ��ж����Ȿ��Ĺؼ�����תǰ���ҵ���ȵ�����
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ�������ˮ������ѧ�������棩 ���ͣ�ѡ����
��4�֣���2015•��ˮ�����κ���y=ax2+bx��1��a��0����ͼ���㣨1��1������a+b+1��ֵ�ǣ� ��
A����3 B����1 C��2 D��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015����б�ҵ��ѧ���ԣ��½���³ľ�������ѧ�������棩 ���ͣ�ѡ����
��4�֣���ͼ����ֱ������ϵxOy�У���A��B�ֱ���x���y�ᣬ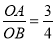 ����AOB�Ľ�ƽ������OA�Ĵ�ֱƽ���߽��ڵ�C����AB���ڵ�D������������
����AOB�Ľ�ƽ������OA�Ĵ�ֱƽ���߽��ڵ�C����AB���ڵ�D������������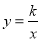 ��ͼ�����C������CDΪ�ߵ������ε����Ϊ
��ͼ�����C������CDΪ�ߵ������ε����Ϊ ʱ��k��ֵ�ǣ� ��
ʱ��k��ֵ�ǣ� ��
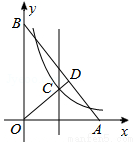
A��2 B��3 C��5 D��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵ�У�OA��OB��sin��OAB=
 ����A��B�ֱ��ڷ���������y1=
����A��B�ֱ��ڷ���������y1=
 ��y2=
��y2=
 ��ͼ���ϣ���k��ֵ�ǣ�������
��ͼ���ϣ���k��ֵ�ǣ�������
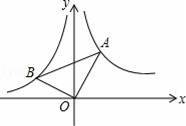

A����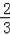
 B����
B����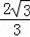
 C����2
C����2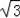
 D��2
D��2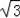

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���м�����ȷ���ǣ�������
A��3m2•m=3m3 B����2m��3=6m3 C����a+b��2=a2+b2 D��3mn��3n=m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ֱ��AB��CD��BEƽ����ABC����CD�ڵ�D�� ��CDB=30������ô��C�Ķ���Ϊ�� ��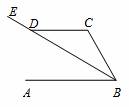
A��150�� B��130�� C��120�� D��100��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij���л���Ϊ�˽���У�������Ķ���ѧ�̿������״�������ȡij���ֳ���ѧ�������˵��顣����������ݻ��Ƴ����²�������ͳ��ͼ���������ͼ���е���Ϣ����������⣺
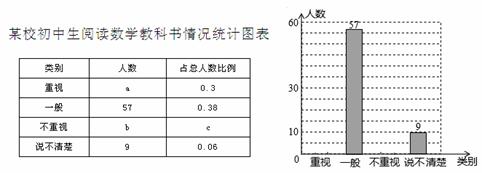
��1��������������������a��b��c��ֵ������ȫͳ��ͼ��
��2������У���г�����2300��������Ƹ�У���������Ķ��̿��顱�ij���������
��3���ٸ��������ͳ�ƽ����̸̸��Ը�У�������Ķ���ѧ�̿������״�Ŀ��������飻
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com