
ΓΨΧβΡΩΓΩ‘ΎΉςΕΰ¥ΈΚ· ΐy1=ax2+bx+c”κ“Μ¥ΈΚ· ΐy2=kx+mΒΡΆΦœσ ±Θ§œ»Ν–≥ωœ¬±μΘΚ
x | Γ≠ | ©¹1 | 0 | 1 | 2 | 3 | 4 | 5 | Γ≠ |
y1 | Γ≠ | 0 | ©¹3 | ©¹4 | ©¹3 | 0 | 5 | 12 | Γ≠ |
y2 | Γ≠ | 0 | 2 | 4 | 6 | 8 | 10 | 12 | Γ≠ |
«κΡψΗυΨί±μΗώ–≈œΔΜΊ¥πœ¬Ν–Έ ΧβΘ§
Θ®1Θ©Εΰ¥ΈΚ· ΐy1=ax2+bx+cΒΡΆΦœσ”κy÷αΫΜΒψΉχ±ξΈΣΘΜ
Θ®2Θ©Β±y1ΘΨy2 ±Θ§Ή‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß «ΘΜ
Θ®3Θ©«κ–¥≥ωΕΰ¥ΈΚ· ΐy1=ax2+bx+cΒΡ»ΐΧθ≤ΜΆ§ΒΡ–‘÷ Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©Θ®0,©¹3Θ©
Θ®2Θ©Β±xΘΦ©¹1ΜρxΘΨ5 ±,Εΰ¥ΈΚ· ΐΒΡ÷Β¥σ”Ύ“Μ¥ΈΚ· ΐΒΡ÷Β
Θ®3Θ©ΫβΘΚΗΟΚ· ΐΒΡΆΦœσΩΣΩΎœρ…œΘΜΒ±x=1 ±Θ§Κ· ΐ”–Ήν¥σ÷ΒΘΜΒ±xΘΦ1 ±Θ§yΥφxΒΡ‘ω¥σΕχΦθ–ΓΘ§Β±xΓί1 ±Θ§yΥφxΒΡ‘ω¥σΕχ‘ω¥σΘΜΕΞΒψΉχ±ξΈΣΘ®1Θ§©¹4Θ©ΘΜΕ‘≥Τ÷αΈΣ÷±œΏx=1Θ°
ΓΨΫβΈωΓΩΘ®1Θ©Ννx=0Θ§«σΒΟyΒΡ ΐ÷ΒΘ§»ΖΕ®”κy÷αΫΜΒψΉχ±ξΦ¥Ω…ΘΜΘ®2Θ©œ»άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ωΕΰ¥ΈΚ· ΐ”κ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘ§«σ≥ωΝΫΚ· ΐΆΦœσΒΡΫΜΒψΘ§ΫχΕχΩ…ΒΟ≥ωΫα¬έΘΜΘ®3Θ©άϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΘΚΩΣΩΎΖΫœρΘ§Ε‘≥Τ÷αΘ§‘ωΦθ–‘÷±Ϋ”ΒΟ≥ω¥πΑΗΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©Εΰ¥ΈΚ· ΐy1=ax2+bx+cΒΡΆΦœσ”κy÷αΫΜΒψΉχ±ξΈΣΘ®0Θ§©¹3Θ©ΘΜΘ®2Θ©”…Χβ“βΒΟΘ§
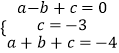 Θ§
Θ§
ΫβΒΟ  Θ°
Θ°
ΓύΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΈΣy=x2©¹2x©¹3=Θ®x©¹1Θ©2©¹4Θ°
ΓΏ“Μ¥ΈΚ· ΐy2=kx+mΒΡΆΦœσΙΐΒψΘ®©¹1Θ§0Θ©Θ§Θ®0Θ§2Θ©Θ§
Γύ ![]() Θ§
Θ§
ΫβΒΟ ![]() Θ°
Θ°
Γύ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΈΣy=2x+2Θ§
»γΆΦΥυ ΨΘ§
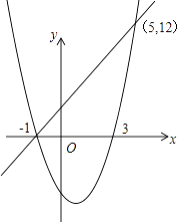
Β±xΘΦ©¹1ΜρxΘΨ5 ±Θ§Εΰ¥ΈΚ· ΐΒΡ÷Β¥σ”Ύ“Μ¥ΈΚ· ΐΒΡ÷ΒΘ°
ΓΨΩΦΒψΨΪΈωΓΩΫβ¥π¥ΥΧβΒΡΙΊΦϋ‘Ύ”ΎάμΫβΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΒΡœύΙΊ÷Σ ΕΘ§’ΤΈ’‘ωΦθ–‘ΘΚΒ±a>0 ±Θ§Ε‘≥Τ÷αΉσ±ΏΘ§yΥφx‘ω¥σΕχΦθ–ΓΘΜΕ‘≥Τ÷α”“±ΏΘ§yΥφx‘ω¥σΕχ‘ω¥σΘΜΒ±a<0 ±Θ§Ε‘≥Τ÷αΉσ±ΏΘ§yΥφx‘ω¥σΕχ‘ω¥σΘΜΕ‘≥Τ÷α”“±ΏΘ§yΥφx‘ω¥σΕχΦθ–ΓΘ°


 ΩΈ ±―ΒΝΖΫ≠Υ’»ΥΟώ≥ωΑφ…γœΒΝ–¥πΑΗ
ΩΈ ±―ΒΝΖΫ≠Υ’»ΥΟώ≥ωΑφ…γœΒΝ–¥πΑΗ ΜΤΗ‘Ψ≠Βδ»ΛΈΕΩΈΧΟœΒΝ–¥πΑΗ
ΜΤΗ‘Ψ≠Βδ»ΛΈΕΩΈΧΟœΒΝ–¥πΑΗ ΤτΕΪ–ΓΧβΉς“Β±ΨœΒΝ–¥πΑΗ
ΤτΕΪ–ΓΧβΉς“Β±ΨœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕΰ¥ΈΚ· ΐy=ax2+bx+cΘ®aΓΌ0Θ©ΒΡΆΦœσ»γΆΦΥυ ΨΘ§œ¬Ν–ΥΒΖ®’ΐ»ΖΒΡΗω ΐ «Θ® Θ©
ΔΌaΘΨ0ΘΜΔΎbΘΨ0ΘΜΔέcΘΦ0ΘΜΔήb2©¹4acΘΨ0ΘΜΔίa+b+c=0Θ°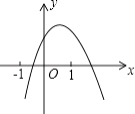
A.1
B.2
C.3
D.4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΕΰ¥ΈΚ· ΐy=ax2+bx+cΒΡΆΦœσΙΐΒψAΘ®©¹1Θ§0Θ©ΚΆΒψCΘ®0Θ§3Θ©Θ§Ε‘≥Τ÷αΈΣ÷±œΏx=1Θ°
Θ®1Θ©«σΗΟΕΰ¥ΈΚ· ΐΒΡΙΊœΒ ΫΚΆΕΞΒψΉχ±ξΘΜ
Θ®2Θ©ΫαΚœΆΦœσΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
ΔΌΒ±©¹1ΘΦxΘΦ2 ±Θ§«σΚ· ΐyΒΡ»Γ÷ΒΖΕΈßΘ°
ΔΎΒ±yΘΦ3 ±Θ§«σxΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCD÷–Θ§ABΘΫ6Θ§ΒψE‘Ύ±ΏCD…œΘ§«“CDΘΫ3DEΘ§ΫΪΓςADE―ΊAEΕ‘’έ÷ΝΓςAEFΘ§―”≥ΛEFΫΜ±ΏBC”ΎΒψGΘ§Ν§ΫαAGΘ§CFΘ§‘ρœ¬Ν–Ϋα¬έΘΚΔΌΓςABGΓ’ΓςAFGΘΜΔΎBGΘΫCGΘΜΔέAGΓΈCFΘΜΔήSΓςEGCΘΫSΓςAFEΘΜΔίSΓςFGCΘΫ![]() ΘΜΤδ÷–’ΐ»ΖΒΡΫα¬έ”–_____Θ°
ΘΜΤδ÷–’ΐ»ΖΒΡΫα¬έ”–_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΨ≈Θ®2Θ©ΑύΉι÷·ΝΥ“Μ¥Έά ΕΝ±»»ϋΘ§ΦΉΓΔ““ΝΫΕ”Ης10»ΥΒΡ±»»ϋ≥…Φ®Θ®10Ζ÷÷ΤΘ©»γœ¬±μΘ®ΒΞΈΜΘΚΖ÷Θ©ΘΚ
ΦΉ | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
““ | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
Θ®1Θ©ΦΉΕ”≥…Φ®ΒΡ÷–ΈΜ ΐ «Ζ÷Θ§““Ε”≥…Φ®ΒΡ÷Ύ ΐ «Ζ÷ΘΜ
Θ®2Θ©ΦΤΥψ““Ε”≥…Φ®ΒΡΤΫΨυ ΐΚΆΖΫ≤νΘΜ
Θ®3Θ©“―÷ΣΦΉΕ”≥…Φ®ΒΡΖΫ≤ν «1.4Ζ÷2 Θ§ ‘ρ≥…Φ®ΫœΈΣ’ϊΤκΒΡ «Ε”Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ’ΐ±»άΐΚ· ΐy=kxΨ≠ΙΐΒψAΘ§ΒψA‘ΎΒΎΥΡœσœόΘ§ΙΐΒψAΉςAHΓΆx÷αΘ§¥ΙΉψΈΣΒψHΘ§ΒψAΒΡΚαΉχ±ξΈΣ3Θ§«“ΓςAOHΒΡΟφΜΐΈΣ3Θ°
Θ®1Θ©«σ’ΐ±»άΐΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©‘Ύx÷α…œΡήΖώ’“ΒΫ“ΜΒψPΘ§ ΙΓςAOPΒΡΟφΜΐΈΣ5ΘΩ»τ¥φ‘ΎΘ§«σΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓςABC÷–Θ§AD «ΓœBACΒΡΫ«ΤΫΖ÷œΏΘ§AE «ΓςABCΒΡΗΏΘ°

Θ®1Θ©»γΆΦ1Θ§»τΓœBΘΫ40ΓψΘ§ΓœCΘΫ62ΓψΘ§«κΥΒΟςΓœDAEΒΡΕ» ΐΘΜ
Θ®2Θ©»γΆΦ2Θ®ΓœBΘΦΓœCΘ©Θ§ ‘ΥΒΟςΓœDAEΓΔΓœBΓΔΓœCΒΡ ΐΝΩΙΊœΒΘΜ
Θ®3Θ©»γΆΦ3Θ§―”≥ΛACΒΫΒψFΘ§ΓœCAEΚΆΓœBCFΒΡΫ«ΤΫΖ÷œΏΫΜ”ΎΒψGΘ§«σΓœGΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΆθάœ ΠΈΣΝΥ¥”ΤΫ ±‘ΎΑύΦΕάο ΐ―ß±»Ϋœ”≈–ψΒΡΦΉΓΔ““ΝΫΈΜΆ§―ß÷–―ΓΑΈ“Μ»Υ≤ΈΦ”ΓΑ»ΪΙζ≥θ÷– ΐ―ßœΘΆϊ±≠ΨΚ»ϋΓ±Θ§Ε‘ΝΫΈΜΆ§―ßΫχ––ΝΥΗ®ΒΦΘ§≤Δ‘ΎΗ®ΒΦΤΎΦδΫχ––ΝΥ5¥Έ≤β―ιΘ§ΝΫΈΜΆ§―ß≤β―ι≥…Φ®ΒΟΖ÷«ιΩω»γΆΦΥυ ΨΘΚ
άϊ”Ο±μ÷–ΧαΙ©ΒΡ ΐΨίΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΗυΨί”“ΆΦΖ÷±π–¥≥ωΦΉΓΔ““Έε¥ΈΒΡ≥…Φ®ΘΚ
ΦΉΘΚΓΓ ΓΓΘΜ““ΘΚΓΓ ΓΓΘ°
Θ®2Θ©Χν–¥Άξ≥…œ¬±μΘΚ
ΤΫΨυ≥…Φ® | ÷–ΈΜ ΐ | ÷Ύ ΐ | ΖΫ≤ν | |
ΦΉ | Έό | 4 | ||
““ | 13 |
Θ®3Θ©«κΡψΗυΨί…œΟφΒΡ–≈œΔΘ§‘Υ”ΟΥυ―ßΒΡΆ≥ΦΤ÷Σ ΕΘ§Αο÷ζΆθάœ ΠΉω≥ω―Γ‘ώΘ§≤ΔΦρ“ΣΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1ΘΚ‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ABΘΫADΘ§ΓœBADΘΫ120ΓψΘ§ΓœBΘΫΓœADCΘΫ90ΓψΘ°EΓΔFΖ÷±π «BCΓΔCD…œΒΡΒψΘ°«“ΓœEAFΘΫ60ΓψΘ°ΧΫΨΩΆΦ÷–œΏΕΈBEΓΔEFΓΔFD÷°ΦδΒΡ ΐΝΩΙΊœΒΘ°
–ΓΆθΆ§―ßΧΫΨΩ¥ΥΈ ΧβΒΡΖΫΖ® «Θ§―”≥ΛFDΒΫΒψGΘ§ ΙDGΘΫBEΘ°Ν§ΫαAGΘ§œ»÷ΛΟςΓςABEΓ’ΓςADGΘ§‘Ό÷ΛΟςΓςAEFΓ’ΓςAGFΘ§Ω…ΒΟ≥ωΫα¬έΘ§ΥϊΒΡΫα¬έ”Π «ΓΓ ΓΓΘΜ

ΧΫΥς―”…λΘΚ
»γΆΦ2Θ§»τ‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ABΘΫADΘ§ΓœBΘΪΓœDΘΫ180ΓψΘ°EΓΔFΖ÷±π «BCΓΔCD…œΒΡΒψΘ§«“ΓœEAFΘΫ![]() ΓœBADΘ§…œ ωΫα¬έ «Ζώ»‘»Μ≥…ΝΔΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΓœBADΘ§…œ ωΫα¬έ «Ζώ»‘»Μ≥…ΝΔΘ§≤ΔΥΒΟςάμ”…ΘΜ
ΒΦ ”Π”ΟΘΚ
»γΆΦ3Θ§‘ΎΡ≥¥ΈΨϋ ¬―ίœΑ÷–Θ§ΫΔΆßΦΉ‘Ύ÷ΗΜ”÷––ΡΘ®O¥ΠΘ©±±ΤΪΈς30ΓψΒΡA¥ΠΘ§ΫΔΆß““‘Ύ÷ΗΜ”÷––ΡΡœΤΪΕΪ70ΓψΒΡB¥ΠΘ§≤Δ«“ΝΫΫΔΆßΒΫ÷ΗΜ”÷––ΡΒΡΨύάκœύΒ»Θ§Ϋ”ΒΫ––Ε·÷ΗΝνΚσΘ§ΫΔΆßΦΉœρ’ΐΕΪΖΫœρ“‘60ΚΘάο/–Γ ±ΒΡΥΌΕ»«ΑΫχΘ§ΫΔΆß““―Ί±±ΤΪΕΪ50ΓψΒΡΖΫœρ“‘80ΚΘάο/–Γ ±ΒΡΥΌΕ»«ΑΫχ1.5–Γ ±ΚσΘ§÷ΗΜ”÷––ΡΙέ≤βΒΫΦΉΓΔ““ΝΫΫΔΆßΖ÷±πΒΫ¥οEΘ§F¥ΠΘ§«“ΝΫΫΔΆß÷°ΦδΒΡΦ–Ϋ«ΈΣ70ΓψΘ§ ‘«σ¥Υ ±ΝΫΫΔΆß÷°ΦδΒΡΨύάκΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com