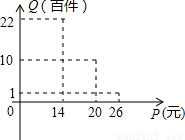
解:(1)根据图象,当14≤P≤20时,
设Q=kP+b,把(14,22),(20,10)代入,得
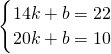
,
解得
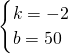
,
则Q=-2P+50;
当20≤P≤26时,
设Q=mP+n,把(20,10),(26,1)代入,得
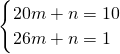
,
解得
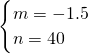
,
则Q=-1.5P+40,
即Q=
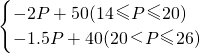
,
若商品的价格应定为P元时,该店刚好能够维持职工生活,
则有100(P-14)Q=3600+2000,分两种情况:
第一种:当14≤P≤20时,即100(P-14)(-2P+50)=5600,解得P
1=18,P
2=21(不合题意,舍去);
第二种:当20≤P≤26时,即100(P-14)(-1.5P+40)=5600,解得P
1=22,P
2=
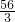
(不合题意,舍去).
答:为使该店刚好能够维持职工生活,商品的价格应定为18元或22元.
(2)设月利润和除职工最低生活费的余额为L,则L=100(P-14)Q-2000.分两种情况:
第一种:当14≤P≤20时,即L=100(P-14)(-2P+50)-3600=-200P
2+7800P-72000,
则当P=
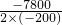
=19.5时,L有最大值,
此时L=
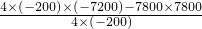
-3600=4050-2000=4050;
第二种:当20≤P≤26时,即100(P-14)(-1.5P+40)-2000=-150P
2+6100P-58000,
则当P=
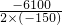
=

时,L有最大值,
此时L=
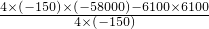
-3600=4016

-2000=2016

.
因为4050>2016

,
所以当P=19.5元时,月利润最大,为4050元.
(3)设可在n年后脱贫,由题意有
12n(4050-3600)≥50000+58000,
解得n≥20,即最早在20年后脱贫.
分析:(1)如果使该店刚好能够维持职工生活,那么该店经营的利润只能保证企业乙的全体职工每个月最低的生活费的开支3600元以及每月所需的各种开支2000元,据此列出方程,从而确定商品的价格;
(2)设月利润和除职工最低生活费的余额为L,列出L与售价P的函数关系式,根据函数性质求出L取最大值时,自变量P的值,从而确定商品的价格;
(3)企业乙脱贫即还清5.8万元的转让价格和5万元的无息贷款,要求最早脱贫时间,由上问P的值,根据题意设可在n年后脱贫,则此n年经营的利润≥50000+58000,求出n的最小值,得出结果.
点评:本题是一道综合题,难度较大.重点考查了一次函数图象和实际应用相结合的问题,能够从图象上准确地获取信息,本题中Q与P的关系是分段的,要注意对应,这是做本题的关键.

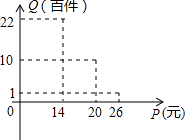 ;②该店月销量Q(百件)与销售价格P(元)的关系如图;③每月需各种开支2000元.
;②该店月销量Q(百件)与销售价格P(元)的关系如图;③每月需各种开支2000元.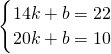 ,
,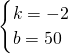 ,
,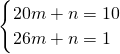 ,
,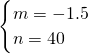 ,
,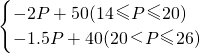 ,
,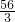 (不合题意,舍去).
(不合题意,舍去).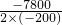 =19.5时,L有最大值,
=19.5时,L有最大值,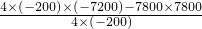 -3600=4050-2000=4050;
-3600=4050-2000=4050;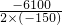 =
= 时,L有最大值,
时,L有最大值,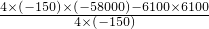 -3600=4016
-3600=4016 -2000=2016
-2000=2016 .
. ,
,

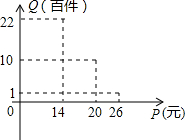 ;②该店月销量Q(百件)与销售价格P(元)的关系如图;③每月需各种开支2000元.
;②该店月销量Q(百件)与销售价格P(元)的关系如图;③每月需各种开支2000元.