
如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.

(1)直线AB的解析式为y=﹣2x+4.
(2)当0<t<2时,S=﹣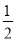 t2+t(0<t<2),
t2+t(0<t<2),
当2<t≤4时,S=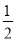 t2﹣t(2<t≤4).
t2﹣t(2<t≤4).
(3)t1=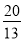 ,H1 (
,H1 (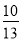 ,
,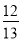 ),
),
t2=20﹣8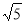 ,H2(10﹣4
,H2(10﹣4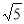 ,4).
,4).
【解析】
试题分析:(1)根据待定系数法即可得到;
(2)过点Q作QF//x轴交y轴于点F,有两种情况:当0<t<2时,PF=4﹣2t,当2<t≤4时,PF=2t﹣4,然后根据面积公式即可求得;
(3)由菱形的邻边相等即可得到.
试题解析:(1)∵C(2,4),
∴A(0,4),B(2,0),
设直线AB的解析式为y=kx+b,
∴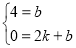 ,
,
解得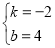
∴直线AB的解析式为y=﹣2x+4.
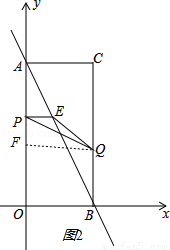
(2)如图2,过点Q作QF⊥y轴于F,
∵PE//OB,
∴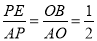
∴有AP=BQ=t,PE= t,AF=CQ=4﹣t,
t,AF=CQ=4﹣t,
当0<t<2时,PF=4﹣2t,
∴S= PE•PF=
PE•PF= ×
× t(4﹣2t)=t﹣
t(4﹣2t)=t﹣ t2,
t2,
即S=﹣ t2+t(0<t<2),
t2+t(0<t<2),
当2<t≤4时,PF=2t﹣4,
∴S= PE•PF=
PE•PF= ×
× t(2t﹣4)=
t(2t﹣4)=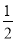 t2﹣t(2<t≤4).
t2﹣t(2<t≤4).
(3)t1=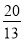 ,H1 (
,H1 ( ,
,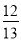 ),
),
t2=20﹣8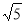 ,H2(10﹣4
,H2(10﹣4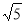 ,4).
,4).
考点:1、待定系数法;2、三角形的面积;3、菱形的性质


科目:初中数学 来源:2013-2014学年北京市顺义区中考二模数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,一次函数 的图象与x轴交于点A,与y轴交于点B,已知
的图象与x轴交于点A,与y轴交于点B,已知 ,
, ,点C(-2,m)在直线AB上,反比例函数
,点C(-2,m)在直线AB上,反比例函数 的图象经过点C.
的图象经过点C.
(1)求一次函数及反比例函数的解析式;
(2)结合图象直接写出:当 时,不等式
时,不等式 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市顺义区中考一模数学试卷(解析版) 题型:选择题
某市在一次扶贫助残活动中,共捐款3 580 000元,将3 580 000用科学记数法表示为( )
A.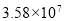 B.
B. C.
C.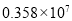 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江绥化卷)数学(解析版) 题型:解答题
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.
(1)求证:CB//PD;
(2)若BC=3,sin∠BPD= ,求⊙O的直径.
,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江绥化卷)数学(解析版) 题型:选择题
如图是一个由多个相同小正方体搭成的几何体的俯视图,图中所标数字为该位置小正方体的个数,则这个几何体的左视图是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江牡丹江卷)数学(解析版) 题型:解答题
如图,在等边△ABC中,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.

(1)当点D在线段BC上,∠NDB为锐角时,如图①,求证:CF+BE=CD;
(提示:过点F作FM∥BC交射线AB于点M.)
(2)当点D在线段BC的延长线上,∠NDB为锐角时,如图②;当点D在线段CB的延长线上,∠NDB为钝角时,如图③,请分别写出线段CF,BE,CD之间的数量关系,不需要证明;
(3)在(2)的条件下,若∠ADC=30°,S△ABC=4 ,则BE= ,CD= .
,则BE= ,CD= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com