
分析 设甲队单独完成这项工程需要x个月,则乙队单独完成这项工程需要(x-4)个月,根据两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的4.8倍建立方程求出其解即可.
解答 解:设甲队单独完成这项工程需要x个月,则乙队单独完成这项工程需要(x-4)个月,由题意,得
x(x-4)=4.8(x+x-4),
解得:x1=1.6(舍去),x2=12.
乙队单独完成这项工程需要12-4=8个月
答:甲队单独完成这项工程需要12个月,乙队单独完成这项工程需要4个月.
点评 本题考查了工程问题的数量关系的运用,列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时根据两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的4.8倍建立方程是关键.


科目:初中数学 来源: 题型:填空题
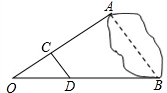 如图,某风景区在建设规划过程中,需要测量两岸码头A、B之间的距离.设计人员在O点设桩,取OA、OB的三等分点C、D,测得CD=25m,则AB=75m.
如图,某风景区在建设规划过程中,需要测量两岸码头A、B之间的距离.设计人员在O点设桩,取OA、OB的三等分点C、D,测得CD=25m,则AB=75m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
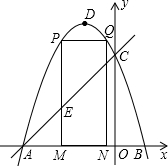 如图,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,3),顶点D的坐标为(-1,4).
如图,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,3),顶点D的坐标为(-1,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com