

分析 (1)由矩形的性质得出AB=CD=6,∠A=90°,由菱形的性质得出BE=DE=AD-AE=8-AE,在Rt△ABE中,由勾股定理得出方程,解方程即可;
(2)连接MC,证出△ACA'是等腰直角三角形,得出∠CA'A=45°,由直角三角形斜边上的中线性质和等腰三角形的性质得出A'M=CM=AM,∠MCA=45°,CM⊥AA',证出∠BCM=∠DA'M,由SAS证明△BCM≌△DA'M,得出BM=DM,∠BMC=∠DMA',由角的雇佣关系证出∠BMD=90°,即可得出结论;
(3)延长AC'、A'C交于点M,由旋转的性质得:BC'=BA,BA'=BC,∠A'BC=∠ABC,∠BA'C=∠BC'A,证出∠BAC=∠BC'A=∠BCA'=∠BA'C,由四边形内角和定理得出∠A'BC'+∠M=180°,证出∠M=90°,得出AC'⊥A'C,证明△ABC'∽△C'BA',得出对应边成比例$\frac{AC′}{A′C}=\frac{AB}{BC}$=$\frac{3}{4}$,即可得出AC'=$\frac{3}{4}$A'C.
解答 (1)解:∵四边形ABCD是矩形,AD=8,CD=6,
∴AB=CD=6,∠A=90°,
∵四边形BEDF是菱形,
∴BE=DE=AD-AE=8-AE,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2,
即62+AE2=(8-AE)2,
解得:AE=$\frac{7}{4}$;
(2)证明:连接MC,如图2所示:
根据题意得:△ABC≌△CDA',∠CDA'=90°,
∴AC=A'C,∠BCA=∠CA'D,∠CA'D+∠A'CD=90°,
∴∠BCA+∠A'CD=90°,
∵点B,C,D在同一条直线上,
∴∠ACA'=90°,
∴△ACA'是等腰直角三角形,
∴∠CA'A=45°,
∵M是AA'的中点,
∴A'M=CM=AM,∠MCA=45°,CM⊥AA',
∵∠BCA=∠CA'D,
∴∠BCA+∠MCA=∠CA'D+∠CA'A,
∴∠BCM=∠DA'M,
在△BCM和△DA'M中,$\left\{\begin{array}{l}{BC=DA'}&{\;}\\{∠BCM=∠DA′M}&{\;}\\{CM=A′M}&{\;}\end{array}\right.$,
∴△BCM≌△DA'M(SAS),
∴BM=DM,∠BMC=∠DMA',
∵∠CMD+∠DMA'=90°,
∴∠CMD+∠BMC=90°,
∴∠BMD=90°,
∴△BMD是等腰直角三角形;
(3)解:AC'⊥A'C,AC'=$\frac{3}{4}$A'C,理由如下:
延长AC'、A'C交于点M,如图3所示:
由旋转的性质得:BC'=BA,BA'=BC,∠A'BC=∠ABC,∠BA'C=∠BC'A,
∴∠BAC=∠BC'A,∠BCA'=∠BA'C,
∴∠BAC=∠BC'A=∠BCA'=∠BA'C,
∵∠BC'A+∠BC'M=180°,
∴∠BA'C+∠BC'M=180°,
∴∠A'BC'+∠M=180°,
∵∠A'BC'=∠ABC=90°,
∴∠M=90°,
∴AC'⊥A'C,
∵∠BAC=∠BC'A=∠BCA'=∠BA'C,
∴△ABC'∽△C'BA',
∴$\frac{AC′}{A′C}=\frac{AB}{BC}$=$\frac{6}{8}$=$\frac{3}{4}$,
∴AC'=$\frac{3}{4}$A'C.
点评 本题是四边形综合题目,考查了矩形的性质、菱形的性质、勾股定理、等腰直角三角形的判定与性质、全等三角形的判定与性质、直角三角形的性质、相似三角形的判定与性质等知识;本题综合性强,有一定难度.


科目:初中数学 来源: 题型:解答题
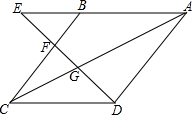 如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD•AE=AC•AG.
如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD•AE=AC•AG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
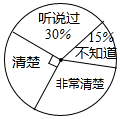 为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形统计图,若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.
为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形统计图,若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2-(m+2)x+3(m-1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=-2x+m+6经过点B,交y轴于点E(0,6).
如图,抛物线y=x2-(m+2)x+3(m-1)与x轴的两个交点为A、B,与y轴交于点C,点D为抛物线的顶点,直线y=-2x+m+6经过点B,交y轴于点E(0,6).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
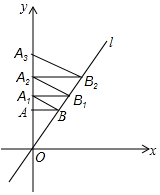 如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,按此作法继续下去,则点A2017的纵坐标为$(\frac{4}{3})^{2017}$.
如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,按此作法继续下去,则点A2017的纵坐标为$(\frac{4}{3})^{2017}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com