
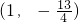 ,与y轴的负半轴交于B点.
,与y轴的负半轴交于B点.
 =1,
=1, =-
=- ,其中a=1,
,其中a=1, ,
, ;
; ,
, );
); ∴CQ=DQ=2.
∴CQ=DQ=2. ,
, ,
, ,
, ),则D(m+2,
),则D(m+2, ),
),
 ,
,
 ,
, ,得:n2-3n-m+1=0,
,得:n2-3n-m+1=0, .
. .
. ,
, ),然后代入即可求出b和c的值,令x=0,求出此时的y,即是点B的纵坐标;
),然后代入即可求出b和c的值,令x=0,求出此时的y,即是点B的纵坐标; ,设C(m,-m-
,设C(m,-m- ),则D(m+2,-m-
),则D(m+2,-m- ),代入抛物线C2的解析式为y=x2-2x+t,求出即可;
),代入抛物线C2的解析式为y=x2-2x+t,求出即可;

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
| S | t3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 过C2顶点M的直线为l,且l与x轴交于点N.
过C2顶点M的直线为l,且l与x轴交于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 3 |

| 1 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com