
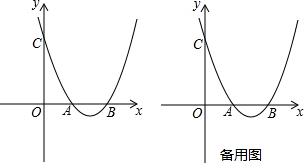
分析 (1)将点A的坐标代入得2+2m+4=0,然后,再求得m的值即可;
(2)先求得点B和点C的坐标,当0<a<4时,过点P作x轴的垂线交BC于D.设直线BC的解析式为y=kx+4,将点B的坐标代入可求得BC的解析式,设点P的坐标为(a,$\frac{1}{2}$a2-3a+4),则点D的坐标为(a,-a+4).然后由S△PBC=S△PCD+S△PBD 可得到△PBC的面积与a的函数关系式,从而可得到△PBC的面积的最大值,当4≤a≤6时,过点P作y轴的垂线交BC于E.则E(3a-$\frac{1}{2}$a2,$\frac{1}{2}$a2-3a+4),PE=$\frac{1}{2}$a2-2a,然后依据S△PBC=S△PCE+S△PBE可得到△PBC的面积与a的函数关系式,从而可得到△PBC的面积的最大值;
(3)作点A关于BC的对称点A′,过点A′作A′F⊥y轴,垂足为F,交BC与点H,依据轴对称的性质可得到A′(4,2)将y=2代入直线BC的解析式可得到点H的坐标.
解答 解:(1)将点A的坐标代入得2+2m+4=0,解得:m=-3.
故答案为:-3.
(2)①当0<a<4时,过点P作x轴的垂线交BC于D.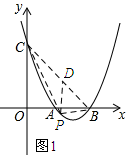
令y=0得:$\frac{1}{2}$x2-3x+4=0,解得x=2或x=4,
∴B(4,0).
设直线BC的解析式为y=kx+4,将点B的坐标代入得:4k+4=0,解得k=-1,
∴BC的解析式为y=-x+4.
设点P的坐标为(a,$\frac{1}{2}$a2-3a+4),则点D的坐标为(a,-a+4).
∴DP=(-a+4)-($\frac{1}{2}$a2-3a+4)=-$\frac{1}{2}$a2+2a.
∴S△PBC=S△PCD+S△PBD=$\frac{1}{2}$×4×(-$\frac{1}{2}$a2+2a)=-(a-2)2+4.
当a=2时 S最大值为4.
②当4≤a≤6时,过点P作y轴的垂线交BC于E.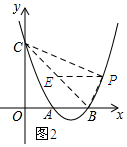
∴E(3a-$\frac{1}{2}$a2,$\frac{1}{2}$a2-3a+4),PE=(a-3a+$\frac{1}{2}$a2)=$\frac{1}{2}$a2-2a.
∴S△PBC=S△PCE+S△PBE=$\frac{1}{2}$×4×($\frac{1}{2}$a2-2a)=(a-2)2-4.
当a=6时 S最大值为12.
综上可知,当0<a≤6时,△PBC面积的最大值为12.
(3)作点A关于BC的对称点A′,过点A′作A′F⊥y轴,垂足为F,交BC与点H.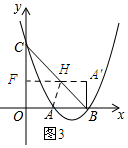
∵BC的解析式为y=-x+4.
∴∠OBC=45°.
∵点A与点A′关于BC对称,
∴∠ABC=∠A′BC=45°,AB=A′B=2,
∴A′(4,2).
在Rt△CFH中,∠FCH=45°,即HF=$\sqrt{2}$HC,
∴点M在整个运动中所用的时间为$\frac{AH}{1}$+$\frac{HC}{\sqrt{2}}$=AH+HF.
∴当点A′、H、F在一条直线上时,所用时间最短.
将y=2代入y=-x+4得:-x+4=2,解得:x=2,
∴点H的坐标为(2,2).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式,轴对称的性质、求得点A′的坐标是解题的关键.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小张对他所在学校的同学使用手机的情况进行了调查,并根据调查的结果制作了如图所示的统计图,由图可知,利用手机玩游戏的同学占30%,则利用手机上网学习的同学所在的扇形的圆心角的度数是72°.
小张对他所在学校的同学使用手机的情况进行了调查,并根据调查的结果制作了如图所示的统计图,由图可知,利用手机玩游戏的同学占30%,则利用手机上网学习的同学所在的扇形的圆心角的度数是72°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
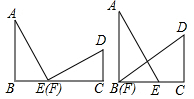 (1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE≌△FCD,AE⊥DF,请你证明:a2+b2=c2;
(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE≌△FCD,AE⊥DF,请你证明:a2+b2=c2;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
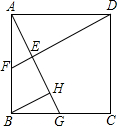 如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得∠ABH=∠CDE.则线段AG、DE与HG之间有什么关系?
如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得∠ABH=∠CDE.则线段AG、DE与HG之间有什么关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com