
分析 根据给定三角形数,罗列出部分an+an+1的值,根据数的变化找出变化规律“an+an+1=(n+1)2”,依此规律即可得出结论.
解答 解:∵a1+a2=1+3=4,a2+a3=3+6=9,a3+a4=6+10=16,a4+a5=10+15=25,a5+a6=15+21=36,…,
∴an+an+1=(n+1)2.
当n=399时,a399+a400=(399+1)2=160000.
故答案为:160000.
点评 本题考查了规律型中的数字的变化类,解题的关键是找出变化规律“an+an+1=(n+1)2”.本题属于基础题,难度不大,解决该题型题目时,根据给定的三角形数,罗列出部分an+an+1的值,根据数的变化找出变化及规律是关键.


科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的四边形是矩形 | B. | 矩形的对角线相等且互相平分 | ||
| C. | 对角线互相平分的四边形是矩形 | D. | 矩形的对角线互相垂直且平分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).
如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
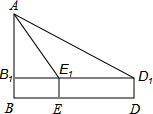 在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)
在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com