
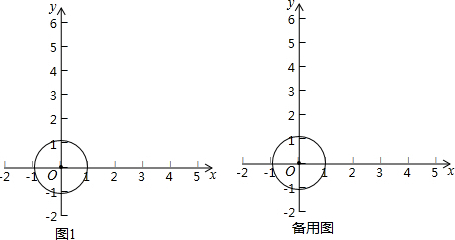
���� ��1�������ڵ�Ķ����֪����ԲC�ڵĵ��Ϊ���ڵ㣬��ԲC��ĵ�������㣬2AB2=PC2-1������AΪPB���е㣬��AB��2���������뾶Ϊ1��ԲC�����ڵ�P����PC�ij���������0��PC��3��PC��1���ֱ����D��E��F����O�ľ��뼴���жϣ����ֱ��y=-x+3��������Ľ�������ֱ�Ϊ��0��3���ͣ�3��0�������ݣ�1�����н��ۿ�֪��P�ĺ������ȡֵ��Χ�ǣ�0��x��3��
��2�����ݣ�1�����п�֪��0��PC��3��PC��1������Ϊ��P���߶�MN���ƶ������Ե�C���Ե�PΪԲ�ģ��뾶Ϊ3��Բ�ڣ��Ҳ������Ե�PΪԲ�ģ��뾶Ϊ1��Բ�ϣ��ٸ��ݵ�C��x���ϣ����ɵó�C�ĺ�����ȡֵ��Χ��
��� �⣺��1���ɶ����֪��
����P�ڡ�C��ʱ��
�ɴ���������֪����P��Ϊ��C�����ڵ㣬
��ʱ��0��PC��1��
����P�ڡ�C��ʱ��
���A��PB���е㣬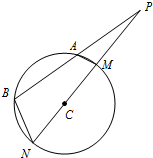
����PC����C�ڵ�M��
�ӳ�PC����C�ڵ�N��
����AM��BN��
�ߡ�AMP+��NMA=180�㣬
��B+��NMA=180�㣬
���AMP=��B��
�ߡ�P=��P��
���AMP�ס�NBP��
��$\frac{PA}{PM}$=$\frac{PN}{PB}$��
��PA•PB=PM•PN��
�ߵ�A��PB���е㣬
��AB=PA��
�֡ߡ�C�İ뾶Ϊ1��
��2AB2=��PC-CM����PC+CN����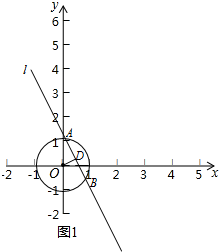
��2AB2=PC2-1��
�֡�AB�ǡ�C���ң�
��AB��2��
��2AB2��8��
��PC2-1��8��
��PC2��9��
��PC��3��
�ߵ�P�ڡ�C�⣬
��PC��1��
��1��PC��3��
����P�ڡ�C��ʱ��
��ʱPC=1�������������⣬
�����������뾶Ϊ1�ġ�C������P��Բ��C�ľ������㣺0��PC��3����PC��1ʱ����PΪ��C�����ڵ㣻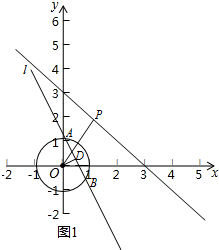
�١�D��$\frac{1}{2}$��$\frac{1}{4}$����
��DO=$\sqrt{��\frac{1}{2}��^{2}+��\frac{1}{4}��^{2}}$=$\frac{\sqrt{5}}{4}$��
��E��0��-$\sqrt{3}$����
��OE=$\sqrt{3}$��
��F��4��0����
��OF=4��
��D��E�ǡ�O�����ڵ㣻
������OD������D��OD�Ĵ��߽���O��A��B���㣻
����x=0����y=-x+3��
��y=3��
��y=0����y=-x+3��
��x=3��
��y=-x+3��������Ľ���Ϊ��0��3���ͣ�3��0��
�����ڵ�P��ֱ��y=-x+3�ϣ��ҵ�P�ǡ�O�����ڵ㣬
��0��PO��3����PO��1
�֡ߵ�P�ڡ�O�⣬
��1��PO��3��
��p�ĺ����귶ΧΪ��0��x��3��
��2��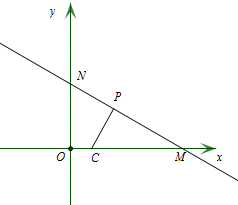 ��x=0����y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��
��x=0����y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��
��y=2$\sqrt{3}$��
��N��0��2$\sqrt{3}$����
��y=0����y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$��
��x=6��
��M��6��0����
�ߵ�P�ǰ뾶Ϊ1�ġ�C�����ڵ㣬
��0��PC��3��PC��1��
���C���Ե�PΪԲ�ģ��뾶Ϊ3��Բ�ڣ��Ҳ������Ե�PΪԲ�ģ��뾶Ϊ1��Բ�ϣ�
�ߵ�C��x���ϣ�
���C�ĺ����귶Χ��ȡֵ��Χ��0��x��9��
���� ���⿼��Բ���ۺ����⣬����ؼ��Ǹ������ڵ�Ķ��壬�ó���P��Բ��C�ľ��뷶Χ�������漰���������ε��������ж���Բ�����ʵ�֪ʶ���ۺϳ̶Ƚϸߣ���Ҫѧ�������������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ֱ�������� | B�� | ƽ���ı��� | C�� | ������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
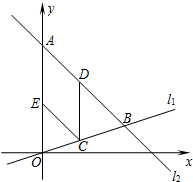 ��ͼ����ƽ��ֱ������ϵ�ڣ���A������Ϊ��0��24 ��������ԭ���ֱ��l1�뾭����A��ֱ��l2�ཻ�ڵ�B����B����Ϊ��18��6����
��ͼ����ƽ��ֱ������ϵ�ڣ���A������Ϊ��0��24 ��������ԭ���ֱ��l1�뾭����A��ֱ��l2�ཻ�ڵ�B����B����Ϊ��18��6�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
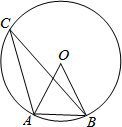 ��ͼ����ABC�ǡ�O�ڽ������Σ���ACB=26�㣬���ABO�Ķ����ǣ�������
��ͼ����ABC�ǡ�O�ڽ������Σ���ACB=26�㣬���ABO�Ķ����ǣ�������| A�� | 64�� | B�� | 52�� | C�� | 54�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� | 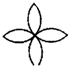 | D�� | 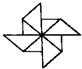 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=3��x-2��2+2 | B�� | y=3��x+2��2-2 | C�� | y=3��x-2��2+2 | D�� | y=3��x+2��2+2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com