练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．下列图形中，既是轴对称图形，又是中心对称图形的是（　　）
    A．B．C．D．

    分析 根据轴对称图形与中心对称图形的概念求解．

    解答 解：A、是轴对称图形，不是中心对称图形，故A错误；
    B、既不是轴对称图形也不是中心对称图形，故B错误；
    C、既是轴对称图形，又是中心对称图形，故C正确；
    D、是中心对图形，不是轴对称图形，故D错误；
    故选：C．

    点评 本题考查了中心对称图形，掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

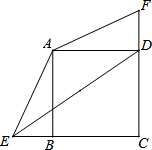    3．已知正方形ABCD中，BC=3，点E、F分别是CB、CD延长线上的点，DF=BE，连接AE、AF，过点A作AH⊥ED于H点．
    （1）求证：△ADF≌△ABE；
    （2）若BE=1，求tan∠AED的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．对于平面直角坐标系xOy中的点P和⊙C，给出如下定义：若存在过点P的直线l交⊙C于异于点P的A，B两点，在P，A，B三点中，位于中间的点恰为以另外两点为端点的线段的中点时，则称点P为⊙C 的相邻点，直线l为⊙C关于点P的相邻线．
    （1）当⊙O的半径为1时，
    ①分别判断在点D（$\frac{1}{2}$，$\frac{1}{4}$），E（0，-$\sqrt{3}$），F（4，0）中，是⊙O的相邻点有D或E；
    ②请从①中的答案中，任选一个相邻点，在图1中做出⊙O关于它的一条相邻线，并说明你的作图过程；
    ③点P在直线y=-x+3上，若点P为⊙O的相邻点，求点P横坐标的取值范围；
    （2）⊙C的圆心在x轴上，半径为1，直线y=-$\frac{\sqrt{3}}{3}x+2\sqrt{3}$与x轴，y轴分别交于点M，N，若线段MN上存在⊙C的相邻点P，直接写出圆心C的横坐标的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，点D为BA延长线上的一点，且∠B=45°，∠D=∠ACB=60°，AB=3$\sqrt{2}$，
    （1）试求BC的长；
    （2）尺规作图：作出△ADC的外接圆⊙O（不写作法，保留作图痕迹），并求出⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，点A（2，0），以OA为半径在第一象限内作圆弧AB，使∠AOB=60°，点C为弧AB的中点，D为半径OA上一动点（不与点O，A重合），点A关于直线CD的对称点为E，若点E落在半径OA上，则点E的坐标为（$2\sqrt{3}-2，0$）；若点E落在半径OB上，则点E的坐标为（$\sqrt{3}-1$，$3-\sqrt{3}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

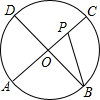    3．如图，AC、BD为圆O的两条互相垂直的直径，动点P从圆心O出发，沿O→C→D→O的路线在半径OC，劣弧$\widehat{CD}$，半径DO上作匀速运动，设运动时间为t秒，∠APB的度数为y度，那么表示y与t之间函数关系的图象大致为（　　）
    A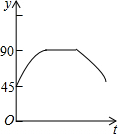．B．C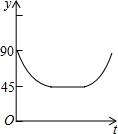．D．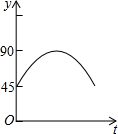

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．某校参加校园青春健身操比赛的16名运动员的身高如表：
     身高（cm） 172 173 175176 
     人数（个） 44 4 4
    则该校16名运动员身高的平均数和中位数分别是（单位：cm）（　　）
    A．173cm，173cmB．174cm，174cmC．173cm，174cmD．174cm，175cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，某电信部门计划修建一条连接B、C两地的电缆，测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B地测得C地的仰角为60°．已知C地比A地高200米，电缆BC至少长多少米？（$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414，结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

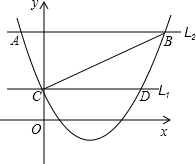    8．如图，抛物线F：y=ax2+bx+c（a＞0）与y轴相交于点C，直线L1经过点C且平行于x轴，将L1向上平移t（t＞0）个单位得到直线L2．设L1与抛物线F的交点为C、D，L2与抛物线F的交点为A、B，连结AC、BC．
    （1）当a=$\frac{1}{2}$，b=-$\frac{3}{2}$，c=1，t=2时，判断△ABC的形状，并说明理由；
    （2）若△ABC为直角三角形，求t的值；（用含a的式子表示）
    （3）在（2）的条件下，若点A关于y轴的对称点A′恰好在抛物线F的对称轴上，连结A′C，BD，若四边形A′CDB的面积为2$\sqrt{3}$，求a的值．

    查看答案和解析>>

    同步练习册答案