
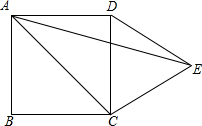
 如图,在正方形ABCD的外侧作等边三角形DCE,则∠EAC的度数为30°.
如图,在正方形ABCD的外侧作等边三角形DCE,则∠EAC的度数为30°. 分析 先根据正方形的性质求得∠DAC的度数,再根据等腰三角形中∠ADE的度数求得∠DAE的度数,最后根据∠EAC=∠DAC-∠DAE,进行计算即可.
解答  解:∵正方形ABCD中,∠DAC=45°,∠ADC=90°
解:∵正方形ABCD中,∠DAC=45°,∠ADC=90°
等边三角形DCE中,∠CDE=60°,
∴∠ADE=150°,
又∵AD=CD=DE,
∴等腰三角形ADE中,∠DAE=$\frac{180°-150°}{2}$=15°,
∴∠EAC=∠DAC-∠DAE=45°-15°=30°.
故答案为:30°.
点评 本题主要考查了正方形的性质以及等边三角形的性质,解题时注意:△ADE为等腰三角形,其底角的度数等于180°减去顶角的度数,再除以2.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
 甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:| 甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
| 乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$或$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在从剩余的13个白色小正方形中选出一个涂成黑色,使涂成黑色的四个小正方形所构成的图形是轴对称图形,则这样的白色小正方形有4个.
如图,是4×4正方形网格,其中已有3个小正方形涂成了黑色,现在从剩余的13个白色小正方形中选出一个涂成黑色,使涂成黑色的四个小正方形所构成的图形是轴对称图形,则这样的白色小正方形有4个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com