
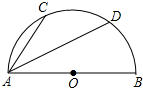
 如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,求AD的长.
如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,求AD的长.| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
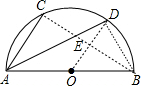 :连接BC、OD、BD,如图,
:连接BC、OD、BD,如图,| AB2-AC2 |
| 1 |
| 2 |
| 1 |
| 2 |
| BE2+DE2 |
| 5 |
| AB2-BD2 |
| 5 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、两名同学5次数学测试成绩的平均分相同,则方差较大的同学成绩更稳定 |
| B、必然事件发生的概率是100%,随机事件发生的概率是50% |
| C、一组数据3,4,4,6,8,5的中位数为4 |
| D、了解湖南卫视“爸爸去哪儿”节目的收视率适合采用抽样调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com