
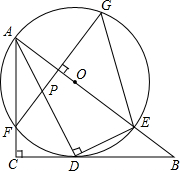
 如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.
如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.| 4 |
| 3 |
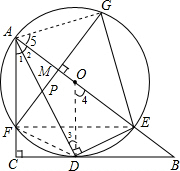 (1)证明:连结OD.
(1)证明:连结OD.| 4 |
| 3 |
| 1 |
| 4 |
| 4 |
| 3 |
| GM |
| AM |
| EM |
| GM |
| 4 |
| 3 |
| AM |
| EM |
| 9 |
| 16 |
| 9 |
| 25 |
| 54 |
| 25 |
| OD |
| AC |
| OB |
| AB |
| CD |
| AO |
| DB |
| OB |
| 3 |
| AC |
| 5 |
| 8 |
| CD |
| 3 |
| 4 |
| 5 |
| 24 |
| 5 |
| 12 |
| 5 |
| PM |
| AM |
| CD |
| AC |
| 1 |
| 2 |
| 1 |
| 2 |
| 27 |
| 25 |
| PM2+AM2 |
| 27 |
| 25 |
| 5 |


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
| A、原式=[-(-7-a-b)][-(7+a+b)]=72-(a+b)2 |
| B、原式=[-(-7+a)+b][-(7+a)-b]=(7+a)2-b2 |
| C、原式=(-7+a+b)[-7-(a+b)]=-72-(a+b)2 |
| D、原式=(-7+a+b)[-7-(a+b)]=72+(a+b)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
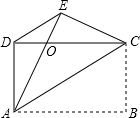 如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
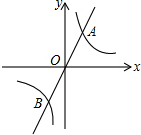 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
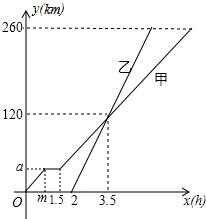
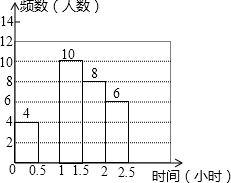 兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.
兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.| 时间(小时) | 频数(人数) | 频率 |
| 0≤t<0.5 | 4 | 0.1 |
| 0.5≤t<1 | a | 0.3 |
| 1≤t<1.5 | 10 | 0.25 |
| 1.5≤t<2 | 8 | b |
| 2≤t<2.5 | 6 | 0.15 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
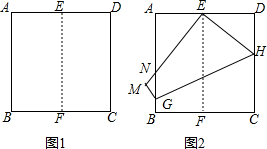 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=
如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com