
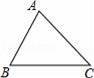
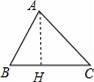
如图,△ABC是锐角三角形,sinC=
 ,则sinA的取值范围是( )
,则sinA的取值范围是( )

A.0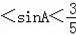
 B.
B.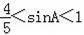
 C.
C.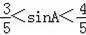
 D.
D.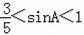

D【考点】锐角三角函数的增减性.
【专题】计算题.
【分析】作AH⊥BC于H,如图,根据正弦定义得到sinC=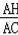
 =
=
 ,则可设AH=4x,AC=5x,利用勾股定理得到CH=3x,所以sin∠HAC=
,则可设AH=4x,AC=5x,利用勾股定理得到CH=3x,所以sin∠HAC=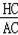
 =
=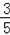
 ,由于∠HAC<∠BAC<90°,然后根据正弦函数为增函数即可得到sin∠BAC的范围.
,由于∠HAC<∠BAC<90°,然后根据正弦函数为增函数即可得到sin∠BAC的范围.
【解答】解:作AH⊥BC于H,如图,
在Rt△ABH中,sinC=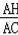
 =
=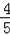
 ,
,
设AH=4x,AC=5x,
所以CH=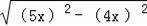
 =3x,
=3x,
所以sin∠HAC=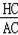
 =
=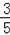
 ,
,
∵∠HAC<∠BAC<90°,
∴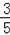
 <sin∠BAC<1.
<sin∠BAC<1.
故选D.

【点评】本题考查了锐角三角函数的增减性:锐角三角函数值都是正值;当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大);当角度在0°≤∠A≤90°间变化时,0≤sinA≤1,1≥cosA≥0.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
在一个不透明的口袋中,有四个完全相同的小球,把它们分别标号为 1、2、3、4,随机地摸取一个小球记下标号后放回,再随机地摸取一个小球记下标号,则两次摸取的小球标号都是 1 的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
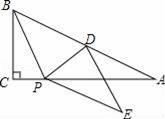
在Rt△ABC中,点D为斜边AB的中点,P为AC边一动点,△BDP沿着PD所在的直线对折,点B的对应点为E.
(1)若BC=5,AC=12,PD⊥AB,求AP的长;
(2)当AD=PE时,求证:四边形BDEP为菱形;
(3)若BC=5,∠A=30°,P点从C点运动到A点,在这个过程中,求E点所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
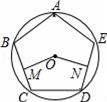

A.108° B.144° C.150° D.166°
查看答案和解析>>
科目:初中数学 来源: 题型:
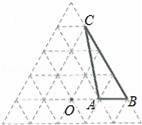
如图是由边长为1的小正三角形组成的网格图,点O和△ABC的顶点都在正三角形的格点上,将△ABC绕点O逆时针旋转120°得到△A′B′C′.
(1)在网格中画出旋转后的△A′B′C′;
(2)求AB边旋转时扫过的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com