
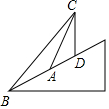
 如图所示,要在斜坡上A、B两点处测量与地面垂直的铁塔CD的高,由A、B两地测得塔顶C的仰角分别为60°和45°,AB的长为40米,斜坡与水平面成30°角,则铁塔CD的高是$\frac{40\sqrt{3}}{3}$米.
如图所示,要在斜坡上A、B两点处测量与地面垂直的铁塔CD的高,由A、B两地测得塔顶C的仰角分别为60°和45°,AB的长为40米,斜坡与水平面成30°角,则铁塔CD的高是$\frac{40\sqrt{3}}{3}$米. 分析 计算∠BCA=15°于是AC=AB=40,求出∠ADC,∠CAD,在△ACD中利用正弦定理得出CD.
解答 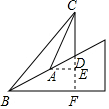 解:延长CD交过A,B的水平线于E,F,
解:延长CD交过A,B的水平线于E,F,
∵∠CAE=60°,∠CBF=45°,∠DBF=30°
∴∠BCF=45°,∠ACE=30°,∠BDF=60°,
∴∠BCA=15°,∠ADC=120°,∠CBA=15°,∠CAD=30°.
∴AC=AB=40,
在△ACD中,由正弦定理得$\frac{AC}{sin∠ADC}$=$\frac{CD}{sin∠CAD}$,
即$\frac{40}{\frac{\sqrt{3}}{2}}=\frac{CD}{\frac{1}{2}}$
解得CD=$\frac{40\sqrt{3}}{3}$.
故答案是:$\frac{40\sqrt{3}}{3}$.
点评 本题考查了正弦定理,解三角形的应用,属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
 完成下面推理过程:
完成下面推理过程:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
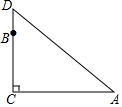 如图,有一个三角形花圃,∠C=90°,AC=20m,BC=10m,两个人同时从点B处出发,以相同速度沿着花圃四周散步,一个沿着BD,DA方向走,另一个沿着BC,CA方向走,结果他们在点A处首次相遇,你能据此求出AD的长吗?试试看.
如图,有一个三角形花圃,∠C=90°,AC=20m,BC=10m,两个人同时从点B处出发,以相同速度沿着花圃四周散步,一个沿着BD,DA方向走,另一个沿着BC,CA方向走,结果他们在点A处首次相遇,你能据此求出AD的长吗?试试看.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com